Varför blir gränsvärdet 1 och inte 0?
Om vi föreställer oss en funktion .
Om man skulle ta skulle man få 1. Men hur kan det var så? Kommer inte nämnaren alltid vara större än täljaren för alla , vilket medför att hela funktionen kommer gå mot 0 när ?
Om vi tittar på ett annat exempel, exempelvis , så skulle denna funktion gå mot 0 när .
I båda exemplen växer nämnaren alltid fortare än täljaren, men ändå blir gränsvärdena inte samma. Varför?
Finns det typ något krav på hur mycket snabbare nämnaren måste växa än täljaren?
Termen lg(x) växer otroligt långsamt då x växer, vilket betyder att detta tillskott till nämnaren blir försumbart i relation till termen 2x.
Om du förkortar uttrycket med x så blir det .
I det uttrycket går nämnarens sista term mot 0 då x går mot oändligheten.
Jag förstår. Men hur ska man veta om tillskottet är försumbart eller inte? Exempelvis i det andra exemplet jag gav så går det hela mot 0, då eftersom tillskottet inte blir försumbart. Men hur ska man avgöra det?
Räkna som vanligt! :)
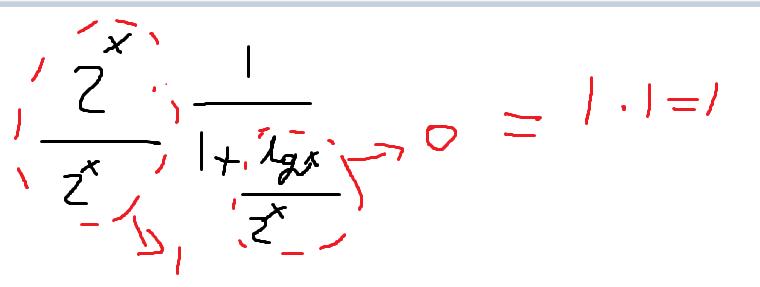
och den andra:
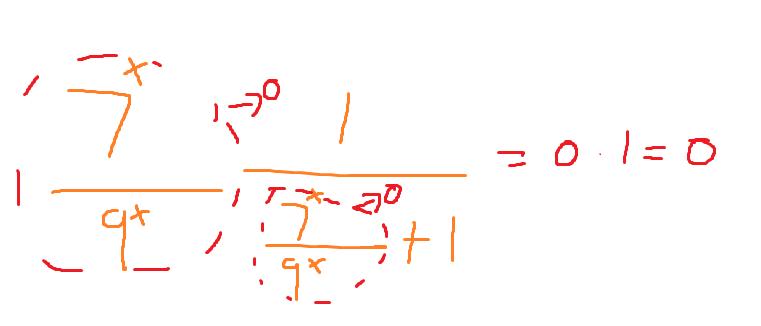
Det är ritat i paint som vanligt, så kanske lite svårläst.
Jag struntade i att skriva limes, men du får inte göra så. :)
Jag hänger med på vad du gör, men på den andra exempelvis: Hur kan du vara säker på att 9x växer tillräckligt mycket snabbare än 7x att skillnaden inte blir försumbar?
Redan för x=2 har du och .
I vilket fall som, så länge 9^x växer lite snabbare än 7^x, så är skillnaden mellan dessa oändligt mycket när x är oändligt stort.
Vi vet också att dessa typer av funktioner växer extremt snabbt. Resultatet förblir densamma om 7^x var (8.5)^x exempelvis.
Efter tillräcklig lång tid så går det mot 0. Det kan ta lååååång tid, men vi tar oss dit tillslut.
så länge 9^x växer lite snabbare än 7^x, så är skillnaden mellan dessa oändligt mycket när x är oändligt stort
Men om vi skulle kolla på exempelvis det första exemplet (innan vi bryter ut eller ändrar) så kommer ju nämnaren där också växa pyttelite snabbare än täljaren. Men där gäller den regeln inte.
lgx växer så sakta i jämförelse. Det blir lite som att dividera dessa talen:
Hm, jag förstår. Men jag tycker det verkar lite flummigt att hänvisa till att det växer "lite snabbare" eller "lite långsammare". Finns det någon hård gräns man kan dra där man säger att skillnaden i tillväxthastighet blir obetydlig?
I fallet med 7^x och 9^x så kan vi det.
men eftersom så är detta strikt avtagande på hela R.
Ah, jag förstår. Så eftersom vi har ett tal mindre än 1 där exponenten blir större och större blir talet mindre och mindre?
Ja, där kan du se kvoten 7/9 som en förändringsfaktor som är mindre än 1.
Finns det någon liknande motivering man kan dra för det första exemplet med logaritmen i nämnaren?
Där tycker jag att du kan ta resonemanget från svar #2.
Värt att nämna är också att denna sorts matematik egentligen inte tillhör matte 3, och om den gör det så har man en miniräknare så kan kan "fuska" lite och se vad som händer grafiskt.
att lgx/x går mot 0 när x går mot oändligheten är ett känt resultat. Kan man visa det med matematik 3 kunskaper? tveksamt. Det enkalste beviset jag kan komma på är att använda l'hopital's regel vilket är långt utanför gymnasie matematik. Vissa saker får du bara ta för givet eller acceptera att du bara kan veta för du sett det grafiskt. :)
Med det sagt, så är #2 en bra motivering till varför gränsvärdet blir vad det blir.




