Mekanik - Varför dämpas den lättare pendeln hårdare än den tyngre?

Halloj!

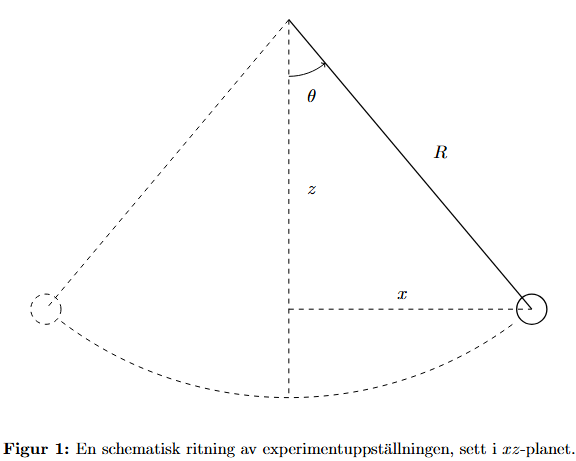
Jag utförde nyligen en laboration på en pendel enligt min figur nedan. Man släppte en pendel med en massa $m$ från en höjd och lät den svänga. Medan pendeln svängde användes ett sofistikerat kamerasystem för att spåra pendelns koordinater över tid.

Vid analys av datan anpassades utslagsvinkeln $\theta$ med regression till en modell på formen:

$\displaystyle \theta\left(t\right)=\theta_0e^{-\zeta\omega t}\sin\left(\omega t+\delta\right)$

där den relevanta konstanten i min fråga här är dämpningskonstanten $\zeta$ , som är ett mått på hur "hårt" pendeln dämpas av icke-konservativa krafter (i vårt fall luftmotstånd).

Vid analys av två pendlar med identiska dimensioner men olika massor visade det sig att den lättare massan dämpades betydligt hårdare än den tyngre massan, till den grad att dess dämpningskonstnat $\zeta_2$ var dubbelt så stor som den tyngres, $\zeta_1$ ! Efter en plot av hur systemens "relativa" mekaniska energier ( $E(t)/E_0$ ) förändrades med tiden syns detta också:

Nu har jag några frågor om detta:

Varför dämpas den lättare massan hårdare än den tyngre, trots identiska dimensioner? Det verkar konstigt eftersom luftmotståndet borde bero på yta, inte massa.
Om man hade släppt två olika tunga massor med identiska dimensioner från en hög höjd ovanför marken på en vindstilla dag, hade då det tyngre massan landat först, eftersom luftmotståndet inte dämpar denna lika hårt?

Det är inte ologiskt. Ofta kan det vara bra att tänka på extremfallen. Tänk dig att du har en jättestark fjäder (högt k) med en jättelätt vikt. Det är rimligt att den då nästan tappar hela sin energi efter någon enstaka svängning. Tvärtom för en svag fjäder med en tung vikt. Det går nog att resonera ganska enkelt med $\mathbf{F}=-k\mathbf{x}$ (för att uppnå en kraft F med större k krävs mindre x osv).

Det är inte ologiskt.

Jag menade förstås att jag har svårt att förstå det haha, verkligheten är ju som den är!

Men jag är rädd att jag inte har samma intuition som du angående fjädersystemet. Jag tycker inte det verkar rimligt eller orimligt att systemet skulle tappa nästan all sin energi för ett jättestort $k$ och en liten massa $m$ . Jag kan inte inordna det intuitivt överhuvudtaget.

Och angående sambandet $\mathbf{F} = -k\mathbf{x}$ finns väl massan inte med här? $k$ är väl en inneboende egenskap hos fjädern?

Kraften som accelererar massan är m g sin $φ$ -c $ρ$ v². Om v är samma och massan blir mindre så förändras denna kraft.

naytte skrev:

Det är inte ologiskt.

Jag menade förstås att jag har svårt att förstå det haha, verkligheten är ju som den är!

Det var verkligen inte menat så. :)

Men jag är rädd att jag inte har samma intuition som du angående fjädersystemet. Jag tycker inte det verkar rimligt eller orimligt att systemet skulle tappa nästan all sin energi för ett jättestort $k$ och en liten massa $m$ . Jag kan inte inordna det intuitivt överhuvudtaget.

För hur k-värdet kommer påverka inbromsningen kan du tänka dig att du hoppar bungeejump. Om linan kan töja sig jättelångt kommer du successivt att bli av med hastigheten i ett bekvämt tempo. Om det är en lina som är jättehård och du väger för lite lär det blir ganska ryckigt och väldigt dämpande.

Och angående sambandet $\mathbf{F} = -k\mathbf{x}$ finns väl massan inte med här? $k$ är väl en inneboende egenskap hos fjädern?

Ja, och beroende på massan kommer också fjäderkraften ha olika storlekar, men jag vet inte riktigt. Hansas resonemang räcker förmodligen som förklaring.

Svara

Visa senaste svar