Varför fungerar fysikaliska modeller i verkligheten?
Hej!
Jag har en något naiv men ändå förbluffande fråga som jag inte riktigt lyckas råda bot på själv. Faktum är att jag inte ens vet om det är en fråga som går att besvara, men jag ställer den ändå. Nedan följer en klassisk fysikerpragmatism:
Små avvikelser från verkligheten i en modell leder till små avvikelser från verkligheten i modellens förutsägelser
Finns det någon underliggande anledning till att denna heuristik fungerar så bra som den gör?
Ett exempel på det jag menar skulle kunna vara den postulatbaserade termodynamiken. Denna modell är formellt sett byggd på antagandet om termodynamisk jämvikt, ett idealiserat tillstånd som inget system i verkligheten kan befinna sig i. Trots att modellen strikt sett endast behandlar system som inte kan existera kan man tillämpa den på system vars tillstånd tillräckligt nära termodynamisk jämvikt. Då erhålles förutsägelser som är nära de empiriska resultaten. Felet i förutsägelsen tillskrivs främst det faktum att systemet faktiskt inte befann sig i sann jämvikt.
Ett annat exempel skulle kunna vara tillståndsekvationen för ideala gaser, . Trots att denna ekvation bygger på antagandet om en idealgas, en idealisering som inte finns i verkligheten, kan man tillämpa den på realgaser som beter sig tillräckligt mycket som idealgaser, och felet mellan hur gasen beter sig i verkligheten och vad idealgasantagandet förutspår tillskrivs det faktum att realgaser inte är idealgaser.
I båda exemplen ovan har vi modeller och formalismer som strikt sett behandlar system under väldigt särskilda antaganden, men som kan tillämpas utanför sina strikta domäner och ändå ge utmärkta förutsägelser, precis i linje med fysikerheuristiken jag nämnde ovan.
Men HUR kan det vara på det här sättet? Det verkar och känns väldigt märkligt att man strikt sett kan modellera något felaktigt men ändå få stor nytta av modellen. Rent principiellt hade man väl kunnat tänka sig att naturen inte vore så snäll och istället avbildade initialtillstånd diskontinuerligt på terminaltillstånd så att små avvikelser från vad modellen kräver gav enorma avvikelser från vad modellen förutsäger?
Det enkla svaret är väl att det visat sig rent experimentellt att vara så i vissa fall och i andra fall inte. Ibland är förenklingar (idealiseringar) användbara, dvs. de förändrar förklaringsvärdet hos modellen relativt lite jämfört med hur mycket de förenklar beräkningar m.m.
Ideala gaslagen är ju t.ex. inte så användbar om det är högt tryck och/eller låga temperaturer, så det finns begränsningar på när den idealiseringen är användbar.
Om du undrar mer generellt varför saker och ting tenderar att bete sig "kontinuerligt", ja då tror jag inte det finns något bra svar. Anledningen till att kontinuitet är så vanligt i teorin beror ju på att det har högt förklaringsvärde för många fenomen och processer i verkligheten. Annars skulle vår teori och våra modeller se annorlunda ut. Det är heller inte alltid så att små förändringar i modellen betyder små skillnader i modellens föeklaringsvärde.
Kort sagt vet vi inte om det vi observerar faktiskt är kontinuerligt, diskret, eller något annat. De modeller vi har utvecklat är helt enkelt dem som visat sig fungera.
Lite mer läsning:
https://physics.stackexchange.com/questions/1324/is-the-world-c-infty
https://en.wikipedia.org/wiki/Idealization_(philosophy_of_science)
Tack för svaret!
Jag har förstått att jag led av extremt selektionsbias när jag författade det här inlägget. Någon förklarade exempelvis
Scientists have spent hundreds of years working out which factors are big, and which are small. Which approximations are basically fine and which are nonsense. Its not that the universe has been fine-tuned so that the small factors have a small effect - its that your scientific education has taught you which factors have a small effect in the problems we look at in our universe.
Och det ligger väl något i det. Det är klart att det verkar som om naturen är fin och kontinuerlig då man nästan uteslutande interagerar med modeller som med framgång beskriver den så. Men det behöver ju inte innebära något särskilt egentligen.
Detta är lite som det att matematiken ofta känns väldigt "verklig" eftersom den är så tillämpbar, men strikt sett finns det oändligt mycket oanvändbart nonsens man hade kunnat definiera inom ZFC och den matematik vi faktiskt använder utgör endast en extremt liten del av all "möjlig" matematik.
Frågan blir nästan lite som att undra "Hur kan jorden vara så bra anpassad efter människan? Den är verkligen perfekt för människan." Detta är ju bakvänt eftersom människan har anpassats efter jorden. Samma gäller för vetenskapliga teorier.
Ja, det är uppenbart nu i efterhand. Samma sak gäller vattenpölen som förbluffat ser sig omkring och drar slutsatsen att det måste finnas en skapare för att hålet han befinner sig i är perfekt format efter honom :)
Hamnade på ett felaktigt tankespår helt enkelt.
Med det sagt finner jag fortfarande det faktum att en idealisering kan fungera överhuvudtaget något mystiskt, men det kanske man helt enkelt bara måste acceptera. Utan idealiseringar hade man inte kunnat modellera någonting alls.
Om du skapar lite data enligt ekvationen där och sedan anpassar en rät linje med hjälp av denna data så kommer du ju definitivt ha anpassat fel modell, men beroende lite på hur den sanna modellen ser ut skulle du fortfarande kunna göra bra förutsägelser, eller hur?
@Hondel, ja, det håller jag med om.
Så skulle inte detta kunna vara den situation du beskriver? Du har en modell som är en rak linje. Men även om ”verkligheten” inte ser ut exakt så kan den vara ”tillräckligt lik” för att den felaktiga modellen ändå ger bra förutsägelser?
Ja, och jag förstår liknelsen. Men frågan är varför naturen är "nästan" en rak linje, varför den beter sig så reguljärt och varför små avvikelser från verkligheten i en modell leder till små avvikelser från verkligheten i modellens förutsägelser. I fallet med termodynamiken kanske vi skulle kunna tänka oss att ett system har parametrar . Denna vektor beskriver allt om ett system vi kan behöva veta.
Låt säga att ett system befinner sig i ett tillstånd som inte är det slutgiltiga tillståndet. Då kommer det av naturen avbildas på ett tillstånd . Se figur nedan
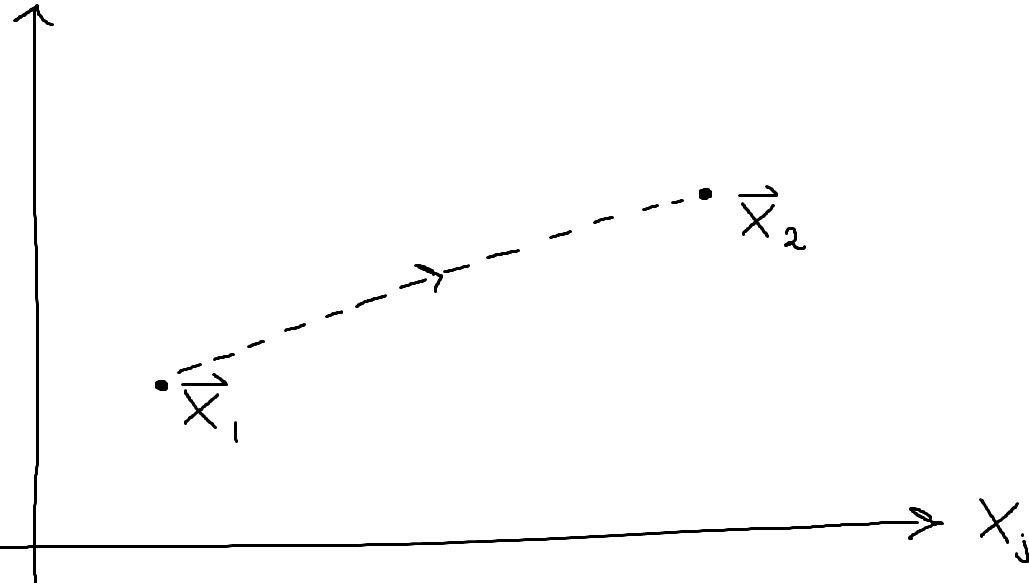
Här ska alltså motsvara , så även om det bara är en axel i den visuella framställningen ska detta föreställa ett hyperrum där varje axel representerar värden på komponenterna i . Linjen som förbinder punkterna är streckad eftersom vi inte vet något om hur systemets tillstånd förändras.
Om vi nu väljer en punkt som är "väldigt nära" , säg , så kommer naturen "avbilda" denna på en punkt , för något litet . Vi kommer alltså ha
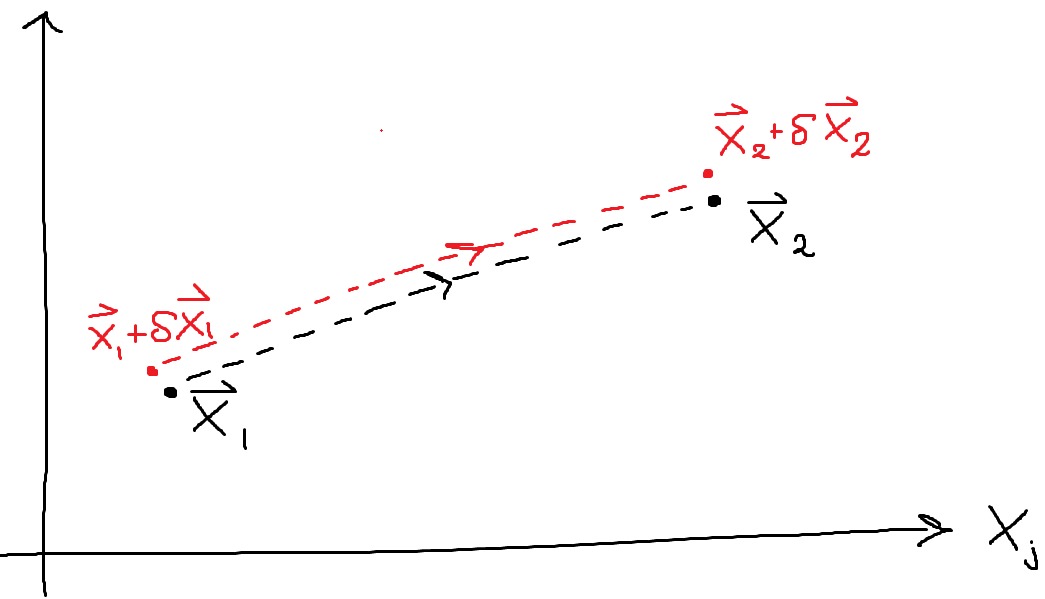
Frågan är nu varför en liten avvikelse i initialtillstånd leder till en liten avvikelse . Finns det något rent principiellt som förhindrar utvecklingen som anges av den lila linjen, där är ett terminaltillstånd som ligger långt bort från ?
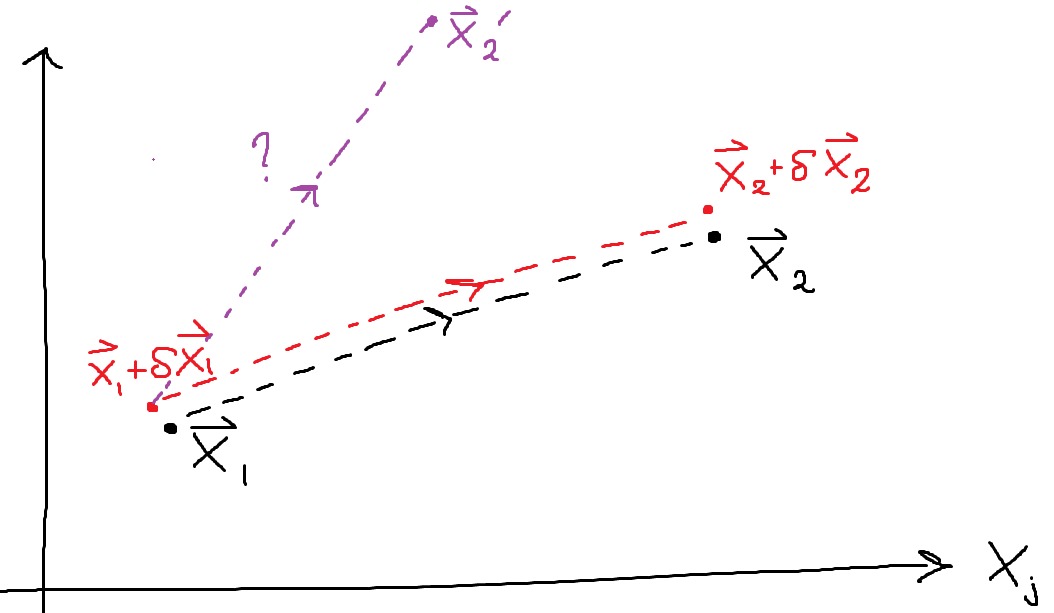
Min fråga är alltså: givet att vi känner till initialtillstånd och terminaltillstånd (vi kan tänka att detta är vad den termodynamiska formalismen förutspår), finns det något som principiellt förhindrar att systemet med initialtillstånd (vi kan tänka att detta är initialtillståndet i verkligheten, utan någon idealisering om "termodynamisk jämvikt".) utvecklas enligt den lila kurvan istället för den röda kurvan, eller är detta något vi vet enligt ren empiri och inget annat?
Tillägg: 9 nov 2025 01:29
Jag vet att detta inte är sant i största allmänhet. Ett exempel skulle kunna vara en penna som precis står på sin spets på ett bord. För infinitesimala förändringar i omgivningen skulle pennan falla ned i vitt skilda diskreta tillstånd som knappast är "nära varandra" i den bemärkelse som avses här.
Som redan sagts: de modeller som har dessa bra egenskaper har vi behållt, de som inte funkat har man varit tvungen att tänka om. Om den verkliga modellen i mitt exempel varit för långt ifrån en rak linje hade man ju konstaterat att det inte funkat och försökt anpassa en annan modell?
Ja men det handlar ju inte bara om modellen här utan också om hur naturen fungerar. Även om vi inte hade haft termodynamiken och dess förutsägelser (den svarta linjen) hade ju en linje med initialtillstånd nära sammanbundits med terminaltillstånd nära . Detta faktum är empiriskt och har ingenting med vår modell att göra. Men finns det någon underliggande princip bakom varför naturen beter sig så så himla ofta eller är det bara rent empiriskt?




