Varför påstår Wolfram Alpha att minimum saknas?
Halloj!
Jag håller på att studera funktionen som definieras av:
för .
Jag tänker att denna funktion trivialt har ett globalt minimum då är en jämn, positiv multipel av . När jag slår detta på Wolfram Alpha får jag däremot:
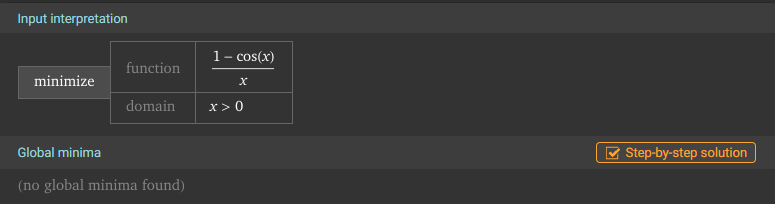
Vad är det som händer här? Visst har väl funktionen ett globalt minimum?
Skumt. Mathematica ger inte heller något om jag inte ber den att göra det numeriskt.
Jag testade att fråga både ChatGPT och Deepseek också och båda insisterar på att göra någon skum Taylorutveckling och beräkna ett gränsvärde runt . Varför begriper jag inte. Båda kommer då dessutom fram till att "minimum inte existerar". Liksom wtf?
Det låter superkonstigt. Funktionen är uppenbart icke-negativ för och det finns värden där den antar värdet 0.
Det som är intressant, i mathematicas fall, är att den ger ett minimum om jag begränsar definitionsmängden ovan: 
Så, i alla fall för mathematica och WA tänkte jag först att det kanske är något problem med att funktionen antar det globala minimit oändligt många gånger? Samtidigt har den inget problem med att spotta ut att har minimum , vilket också sker oändligt många gånger.
Jag tror också att det handlar om att motorn kör fast någonstans när den ska hitta eller verifiera alla de onädligt många minimipunkterna. WA misslyckas till exempel även med cos^2(x)/x och x(1-cos(x)).
Det är i någon mån förståeligt att det är svårt att hantera oändligt många punkter, men det märkliga är precis som AlexMu säger att den kan hantera andra (och vid första anblicken mer komplicerade) periodiska funktioner, t.ex. tan^2(x)cos^2(x)sin^2(x), abs(cos(x)-1) och (cos(x)-1)^2 – och till och med produkten av alla dessa tre funktioner!
oggih skrev:Jag tror också att det handlar om att motorn kör fast någonstans när den ska hitta eller verifiera alla de onädligt många minimipunkterna. WA misslyckas till exempel även med cos^2(x)/x och x(1-cos(x)).
Det är i någon mån förståeligt att det är svårt att hantera oändligt många punkter, men det märkliga är precis som AlexMu säger att den kan hantera andra (och vid första anblicken mer komplicerade) periodiska funktioner, t.ex. tan^2(x)cos^2(x)sin^2(x).
Spontan gissning är att dina exempel på de mer komplicerade funktionerna faktiskt är periodiska, till skillnad från de andra exemplen som .
Den kanske specifikt har problem med funktioner som inte är periodiska som har en periodisk funktion som ”del-funktion” (och når minimi oändligt många gånger)?
Det är en mycket bra poäng!
Man skulle kunna gissa att WA drar någon slags gräns vid icke-periodiska funktioner med oändligt många extrempunkter, och helt enkelt inte ens försöker sig på att bestämma ett globalt minimum för sådana.
Så kan det vara! Låter rimligt. Skulle vara intressant att veta exakt vad som händer här bakom kulisserna.
Utvecklarna kanske svarar på sådana frågor.
Prova att lägga upp ett inlägg här:
Om man bara deriverar för minima (ev två ggr) får man villkoret hsinh+cosh=1 som mycket riktigt ger extremvärden för n 2pi (cos är 1 och sin är 0) Funktionen är då 0. Den alltid positiv. Vill man se den visas den lätt på geogebra
I en högeromgivning till origo är f >0 och avtagande när h—>0. Den hade fått ett minimum om 0 hade ingått i Df,, vilket ej är fallet här.
Tomten skrev:I en högeromgivning till origo är f >0 och avtagande när h—>0. Den hade fått ett minimum om 0 hade ingått i Df,, vilket ej är fallet här.
Vad lustigt! Jag tolkade också frågan på det sättet först, men det är inte det som de pratar om. Rita grafen i WA, så ser du nog vad det här handlar om.
Jag lutar åt att utvecklarna på WA får förklara. Troligen har det med ickeperiodicitet och många nollställen att göra.





