Vektor
Hej! Jag fastnat på denna uppgift,, hur ska och vilken formel ska man använda??
tack i förhand!
Innan du börjar fundera på vilken formel du skall använda: Har du ritat?
Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
Smaragdalena skrev:Innan du börjar fundera på vilken formel du skall använda: Har du ritat?
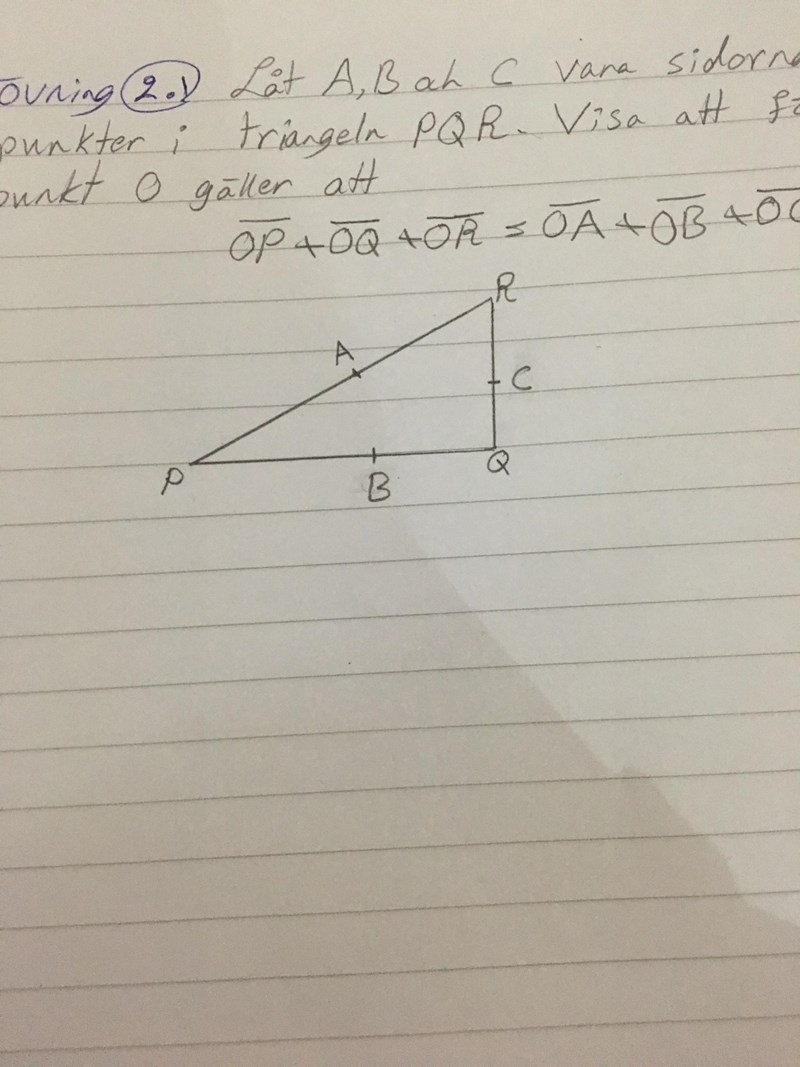
Nej faktiskt inte! Jag skulle rita en triangel med PQR, men sen jag tänkte var ska jag placera ABC?
lava skrev:Smaragdalena skrev:Innan du börjar fundera på vilken formel du skall använda: Har du ritat?
Nej faktiskt inte! Jag skulle rita en triangel med PQR, men sen jag tänkte var ska jag placera ABC?
På sidornas mittpunkter, står det.
var ska jag placera ABC?
Där det står i uppgiften: Mitt på vardera triangelsidan.
Affe Jkpg skrev:Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
P.s.s. med V.L.
Affe Jkpg skrev:Affe Jkpg skrev:Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
P.s.s. med V.L.
det är OA = - AB + OB ?
Smaragdalena skrev:var ska jag placera ABC?
Där det står i uppgiften: Mitt på vardera triangelsidan.
Jag har ritat triangelen rätt right?
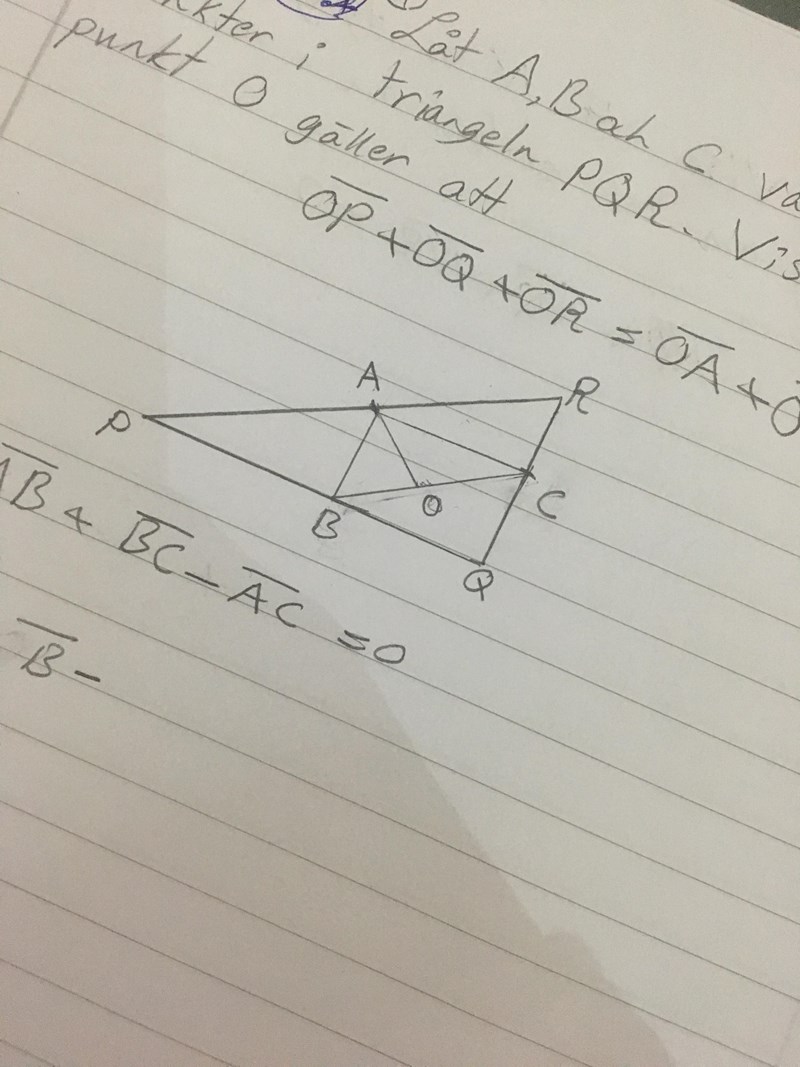
Jag kom fram till de två trianglar,, vad är nästa steg?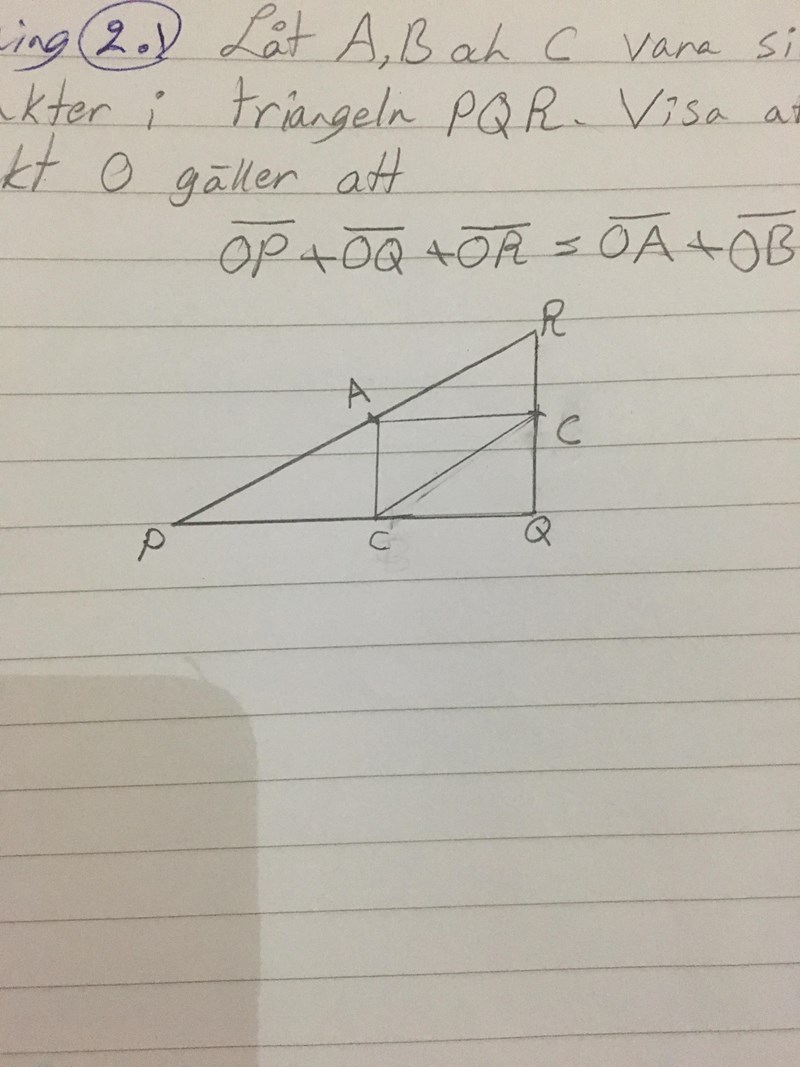
Triangeln ser bra ut. Var har du punkten O?
Smaragdalena skrev:Triangeln ser bra ut. Var har du punkten O?
Denna är jag lite osäker på🤷🏻♀️
lava skrev:Affe Jkpg skrev:Affe Jkpg skrev:Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
P.s.s. med V.L.
det är OA = - AB + OB ?
P.s.s. med V.L.
lava skrev:Jag kom fram till de två trianglar,, vad är nästa steg?
Rita vektor-pilar i din figur, så blir det lättare. Sedan har du skrivit "C" två gånger i figuren.
Affe Jkpg skrev:lava skrev:Jag kom fram till de två trianglar,, vad är nästa steg?
Rita vektor-pilar i din figur, så blir det lättare. Sedan har du skrivit "C" två gånger i figuren.
Ena är B självklart☺️
Du skall visa något som skall gälla för varje punkt O, så sätt ut en precis var som helst - i den lilla triangeln, i den stora triangeln eller utanför. (Det vore opraktiskt att placera punkten utanför pappret, men det skulle stämma då också!)
Smaragdalena skrev:Du skall visa något som skall gälla för varje punkt O, så sätt ut en precis var som helst - i den lilla triangeln, i den stora triangeln eller utanför. (Det vore opraktiskt att placera punkten utanför pappret, men det skulle stämma då också!)
Kan man placera O där?
Affe Jkpg skrev:lava skrev:Affe Jkpg skrev:Affe Jkpg skrev:Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
P.s.s. med V.L.
det är OA = - AB + OB ?
P.s.s. med V.L.
Tack! Men har jag gjort den första triangeln rätt?
lava skrev:Smaragdalena skrev:Du skall visa något som skall gälla för varje punkt O, så sätt ut en precis var som helst - i den lilla triangeln, i den stora triangeln eller utanför. (Det vore opraktiskt att placera punkten utanför pappret, men det skulle stämma då också!)
Kan man placera O där?
Den placeringen av "O" känns inte särskilt generell. Placera "O" någonstans utanför den stora triangeln.
Affe Jkpg skrev:lava skrev:Smaragdalena skrev:Du skall visa något som skall gälla för varje punkt O, så sätt ut en precis var som helst - i den lilla triangeln, i den stora triangeln eller utanför. (Det vore opraktiskt att placera punkten utanför pappret, men det skulle stämma då också!)
Kan man placera O där?
Den placeringen av "O" känns inte särskilt generell. Placera "O" någonstans utanför den stora triangeln.
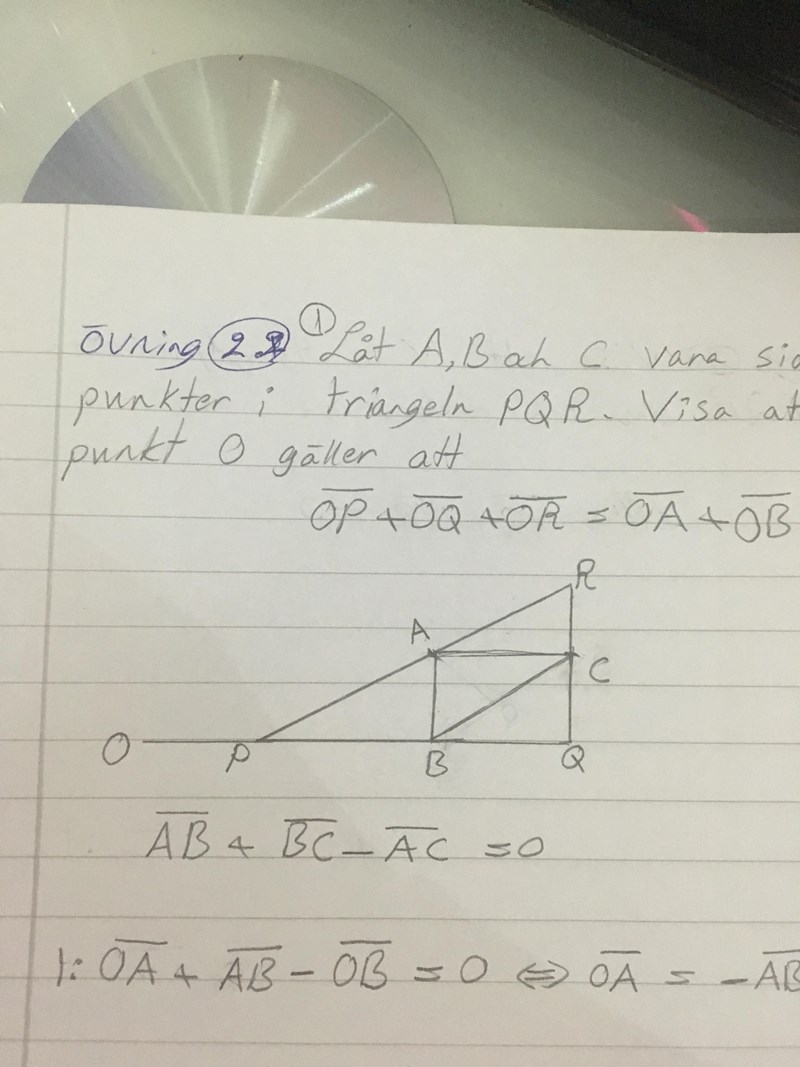
Ser det okej ut?
Och varför ska "O" placeras på en förlängning av en linje! Det blir ju svårt att betrakta överlappande vektorer då!
Affe Jkpg skrev:Och varför ska "O" placeras på en förlängning av en linje! Det blir ju svårt att betrakta överlappande vektorer då!
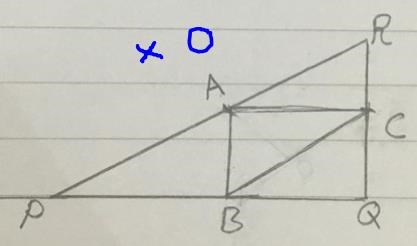
Därför jag placerat det inne på den lilla triangeln!?
Jag ser fortfarande inga vektorer, bara linjer i dina trianglar.
lava skrev:Affe Jkpg skrev:lava skrev:Affe Jkpg skrev:Affe Jkpg skrev:Om du ser sidorna i en triangel som tre vektorer som summeras, vad blir summan av dessa tre?
Hur kan du använda det i V.L. resp. H.L.?
P.s.s. med V.L.
det är OA = - AB + OB ?
P.s.s. med V.L.
Tack! Men har jag gjort den första triangeln rätt?
Jo, den första är rätt :-)
PA havererade, när jag la in den senaste bilden. Jag fick i alla fall ordning på föregående inlägg med bilden....
Jag frstår inte din fråga. Det här skall gälla för alla trianglar PQR så du kan rita den triangeln hur som helst, bara ABC har sina hörn på sidornas mittpunkter.
Smaragdalena skrev:Jag frstår inte din fråga. Det här skall gälla för alla trianglar PQR så du kan rita den triangeln hur som helst, bara ABC har sina hörn på sidornas mittpunkter.
ABC behöver inte ens sitta på sidornas mittpunkter.
Hej!
Vektoraddition för triangelns hörn med startpunkt i O ger
Vektoraddition för triangelsidornas mittpunkter med start i O ger
Du får bra tips av Affe i
En figur kan se ut så här:
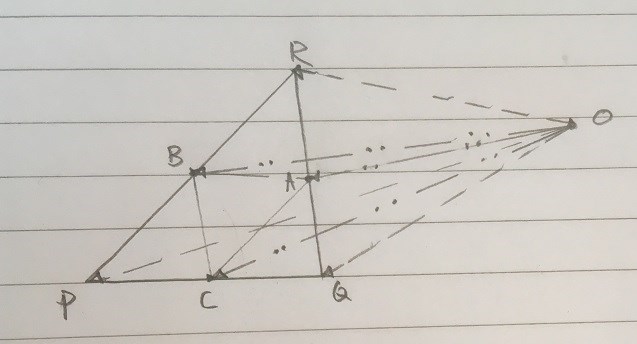
Om du läser så ser du det tydligt i figuren.
Se även Albikis förklaring
Affe Jkpg skrev:ABC behöver inte ens sitta på sidornas mittpunkter.
Är du säker på det?
Albiki skrev:Hej!
Vektoraddition för triangelns hörn med startpunkt i O ger
Vektoraddition för triangelsidornas mittpunkter med start i O ger
Tack jag förstår förklaringen, men är detta ett svar (bevis)?
Hoppas att någon visar beviset.
Mitt förslag är att titta på figuren.
Triangel ABC är likadan som PCB med lika stora sidor. Man kan prova olika trianglar, men det blir alltid så.
Skriv om HL som
OA + OB + OC = (OP + PA) + (OQ + QB) + (OR + RC) = (OP + OQ + OR) + (PA + RC + QB)
Beviset är klart om
(PA + RC + QB) = nollvektorn.
Använd att PA = PR/2, RC = RQ/2, QB = QP/2, så
(PA + RC + QB) = (PR + RQ + QP)/2 = (PQ + QP)/2 = nollvektorn.
Tack Dr.G
Det blev lite över min kunskapsnivå, men det var intressant att repetera gamla vektorkunskaper och det uppmuntrar mig definitivt att läsa vidare. Det känns inte som något oöverkomligt i alla fall.
I vilken kurs lär man sig sådant här? Med bara gymnasiekunskaper känner inte jag igen mig riktigt i alla fall.