Vem har rätt? A eller B
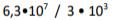 =
=
A) 2,1 x 10^10
B) 2,1 x 10^4
Hej och välkommen till PA!
Vad tror du själv?
Hej.
Du kan skriva uttrycket som , vilket kan skrivas som
Blev det lättare att se vad svaret ska vara då?
Tillägg: 3 apr 2024 16:27
Jag tolkade uttrycket fel och läste in parenteser där det inte står några.
Rätt tolkning bör vara (6,3•107/3)•103.
Se dock diskussion kring detta i efterföljande svar.
Yngve skrev:Du kan skriva uttrycket som , vilket kan skrivas som
Blev det lättare att se vad svaret ska vara då?
Eftersom multiplikation och division har samma prioritet, är jag sugen på att räkna från vänster till höger. Jag är dock inte mattelärare, men eftersom det i mina ögon är dubbeltydigt, skulle jag nog ändå välja att göra så.
Då blir det istället:
Jag måste erkänna att jag gärna "ser" paranteser, ungefär som Yngve skriver, men hittar inget stöd för det när jag söker på nätet:
Om det stått hade jag inte tvekat. Då hade jag räknat den implicita/sammanskrivna multiplikationen först.
Någon som vet mer får gärna bekräfta, alternativt slå mig på fingrarna. ;-)
sictransit skrev:Eftersom multiplikation och division har samma prioritet, är jag sugen på att räkna från vänster till höger. [...]
Då blir det istället:
Det stämmer.
Jag måste erkänna att jag gärna "ser" paranteser, ungefär som Yngve skriver,
Rätt av dig, fel av mig. Jag '"såg" parenteser där de inte finns
sictransit skrev:Yngve skrev:Du kan skriva uttrycket som , vilket kan skrivas som
Blev det lättare att se vad svaret ska vara då?
Eftersom multiplikation och division har samma prioritet, är jag sugen på att räkna från vänster till höger. Jag är dock inte mattelärare, men eftersom det i mina ögon är dubbeltydigt, skulle jag nog ändå välja att göra så.
Då blir det istället:
Jag måste erkänna att jag gärna "ser" paranteser, ungefär som Yngve skriver, men hittar inget stöd för det när jag söker på nätet:
Om det stått hade jag inte tvekat. Då hade jag räknat den implicita/sammanskrivna multiplikationen först.
Någon som vet mer får gärna bekräfta, alternativt slå mig på fingrarna. ;-)
Skulle du tveka om det stod 63 000 000/3 000? Det är precis samma sak som i frågan, bara skrivet i grundpotensform.
Smaragdalena skrev:Skulle du tveka om det stod 63 000 000/3 000? Det är precis samma sak som i frågan, bara skrivet i grundpotensform.
Nej det är inte samma sak.
Det jag inte insåg var att frågan gäller om det som står där ska tolkas som (6,3•107)/(3•103) eller som (6,3•107/3)•103.
Enligt räkneordningen är det det sistnämnda.
Jag kan inte tolka frågan som något annat än en kvot av två tal i grundpotensform.
Menar du att multiplikationstecknet ska tolkas på ett särskilt sätt när ett tal är skrivet i grundpotensform, så att denna multiplikation har högre prioritet än division?
Ja, man kan väl säga att ett tal skrivet i grundpotensform har sina egna parenteser runt sig.
Om du räknar t ex 1/103 på en räknare och använder knappen EE (eller exp eller vad man nu har för att skriva grundpotensform) så får man rätt svar utan att sätta nämnaren i parentes. Om man använder t ex knappen 10x måste man, förutom att man behöver skriva ett multiplikationstecken, sätta nämnaren i parentes.
Smaragdalena skrev:Ja, man kan väl säga att ett tal skrivet i grundpotensform har sina egna parenteser runt sig.
Här håller jag inte alls med dig.
Det kan inte vara upp till var och en huruvida ett givet uttryck, t.ex. 4,7•103 ska tolkas som en produkt av de två faktorerna 4,7 och 103 eller som en "enhet", dvs som (4,7•103).
Det enda rimliga är att det ska tolkas precis som det står, dvs som det förstnämnda.
Om du räknar t ex 1/103 på en räknare och använder knappen EE (eller exp eller vad man nu har för att skriva grundpotensform) så får man rätt svar utan att sätta nämnaren i parentes.
Ja, det stämmer, men det beror på att "EE" betyder "Enter Exponent" och är ett kortare sätt att skriva "*10^". Det knyter ihop mantissan med tiopotensen på det sätt som du läser in i uttrycken givna i uppgiften.
Dvs 4,7EE3 betyder (4,7•103).
Men jag anser att det inte är så det står i uppgiften.
Om man använder t ex knappen 10x måste man, förutom att man behöver skriva ett multiplikationstecken, sätta nämnaren i parentes.
Ja, och det är så jag anser att det står i uppgiften.



