Vilka funktioner är väntevärdesriktiga skattare av my?
Halloj!
Jag sitter med uppgiften nedan:
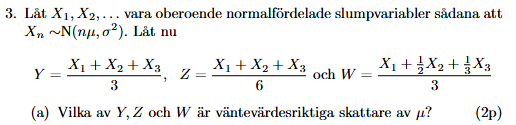
Så som jag förstår det är en parameterskattning väntevärdesriktig om dess väntevärde ger den sökta parametern. Jag förstår däremot inte hur man ska beräkna t.ex. . Definitionen jag har sett av väntevärde för en kontinuerlig slumpvariabel är:
där är täthetsfunktionen för .
Jag förstår däremot inte vad "" blir i detta sammanhang?
Det är täthetsfunktionen, och den kan du kolla upp eftersom du vet att slumpvariabeln är normalfördelad.
Jag förstår tyvärr inte.
Är det meningen att man med hjälp av uttrycken ska ta fram ett uttryck för fördelningen på t.ex. ?
Du kan använda dig av att väntevärdet av en summa av variabler är en summa av väntevärden. Alltså att . Det följer från definitionen av väntevärde som du skrivit upp, och gäller oavsett fördelning hos de olika variablerna.
Tillägg: 17 maj 2025 17:21
Och dessutom gäller att . Det är ännu enklare att bevisa från definitionen av väntevärden
Så:
och sedan använder vi
?
Låter väl bra!
Hmm.
Finns det något knep här för att se vilka av parameterskattningarna som är väntevärdesriktiga? Med definitionen av väntevärdet blir det rätt krångligt...
Jag kommer fram till t.ex:
om jag har tänkt rätt. Men detta är ju väldigt jobbigt att beräkna för bara 2p. Det jag försöker göra är alltså att beräkna väntevärdena för att se ur vilken faller ut. Men uppenbarligen måste det finnas något enklare sätt.
Du vet väl vad väntevärdet av en normal-fördelning är, det behöver du väl inte räkna ut explicit med integralen?
Just det ja! Väntevärdet av en normalfördelad slumpvariabel är väl helt enkelt ?
Exakt. (Notera dock att de olika variablerna har lite olika medelvärden, men det kanske du redan sett)
När du är klar med uppgiften kan det ju vara ett bra test att själv härleda de två räknereglerna du använt, att de gäller oavsett fördelning på de olika variablerna
Okej, då får jag:
Detta innebär alltså att inte är en väntevärdesriktig skattare men att och är det. Är det rätt resonerat?
Det tycker jag låter riktigt.
En till fråga man kan ställa sig: hur hade uppgiften förändrats om fördelningen av var okänd, och att man bara visste att ?
Hade den förändrats överhuvudtaget? Resonemanget ovan kan vi väl använda trots att vi inte känner fördelningen av ...? Det som gjorde det relevant att veta att det var en normalfördelning var väl just egenskapen men om vi får detta i uppgiften behöver vi väl inget mer?
Jag håller med dig. Ingen av de räkneregler du använde baserades på normalfördelningen, och det vi i slutändan behövde var respektive väntevärde.



