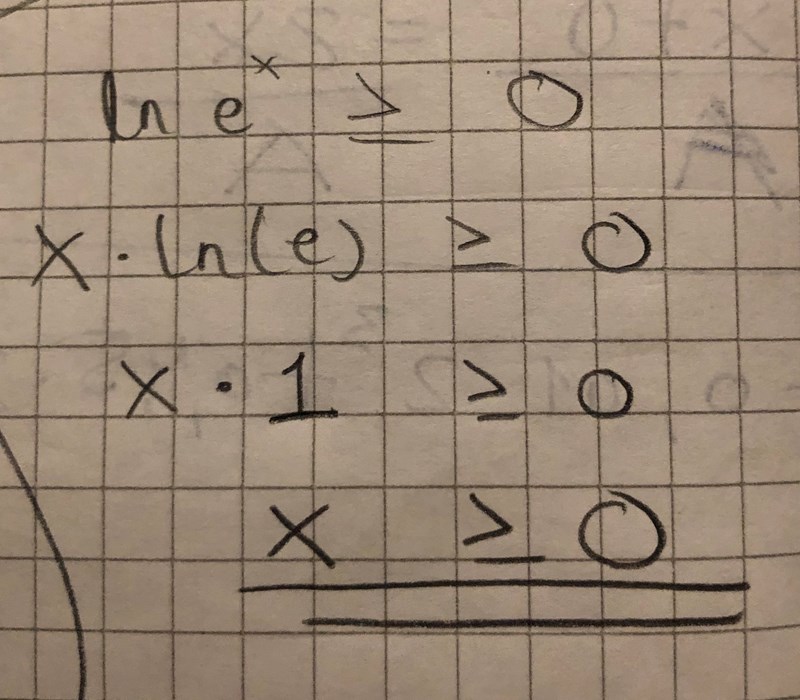Vilka värden på x
Frågan jag ska besvara lyder ”För vilka värden på x är funktionerna f(x)=(e^x)-x och f(x)=(e^x)+x växande?”
 Så långt lyckas jag. Hur kommer jag vidare?
Så långt lyckas jag. Hur kommer jag vidare?
Derivatan av är . Du kan bara använda regeln för derivator av x-potenser på just sådana. Det här är en exponentialfunktion.
Du blandar ihop deriveringsreglerna för och .
Derivatan av är .
Sen en liten detalj: är växande där
Vänta nu hänger jag inte med. Vad är skillnaden? Gäller deriverings reglerna inte för alla tal oavsett vilka det är?
Det är x som är variabeln, så det är viktigt var x står någonstans.
f(x)=e^x -x
derivatan av f(x) blir alltså
f’(x)= x* e^x -1
Nej, derivatan av e^x är fortfarande e^x.
Varför? Vad för regeler finns det gällande derivata generellt sätt?
Alla funktioner du förväntas derivera får du lära dig derivatan av (och ibland härleda den som övning): potensfunktioner, exponentialfunktioner, logaritmer och trigonometriska funktioner. Funktioner som är sammansatta av dessa kan man derivera med produktregeln och kedjeregeln. Ibland får man skriva om funktionen på ett smart sätt, som x^x.
Lisa14500 skrev:Varför? Vad för regeler finns det gällande derivata generellt sätt?
Här finns de du behöver och några till.
Okej då är jag med på att derivatan av e^x är e^x
Derivatan av e^x är 1*e^x * ln(e)= e^x.
Du ska alltså använda kedjeregeln här. Först deriverar du x och det blir 1. Sen deriverar du e^x och du får e^x *ln(e). Ln(e) = 1 så egentligen får du bara e^x.
f’(x)= e^x -1
f’(x)=e^x +1
Funktionen är växande då funktionens derivata är Större eller lika med 0
EDIT - jag läste fel
Nej det stämmer inte. Varifrån får du +1?
- Derivatan av är
- Derivatan av är
Det betyder att derivatan av är
Yngve skrev:Nej det stämmer inte. Varifrån får du +1?
- Derivatan av är
- Derivatan av är
Det betyder att derivatan av är
Ja, men det är två olika f samtidigt, och de har de derivator som Lisa skrev. (Funktionerna borde ha kallats olika saker i uppgiften, t.ex. f och g.)
Vad som återstår är att ta reda på när derivatorna är större än 0.
Oj. Jag läste fel. Tack för påpekandet.
Laguna skrev:Yngve skrev:Nej det stämmer inte. Varifrån får du +1?
- Derivatan av är
- Derivatan av är
Det betyder att derivatan av är
Ja, men det är två olika f samtidigt, och de har de derivator som Lisa skrev. (Funktionerna borde ha kallats olika saker i uppgiften, t.ex. f och g.)
Vad som återstår är att ta reda på när derivatorna är större än 0.
Är det inte då lutningen är större än 0?
Du ska lösa olikheten för de båda funktionerna.
Okej.
e^x -1 > 0
e^x> 1
ln (e^x) > ln 1
ln (e^x) > 0
alltså e^x > 0
ln (e^x) > 0 stämmer, men inte nästa rad. Vad kan du förenkla ln(e^x) till?
Vad ska jag göra?
förenkla ln(e^x)
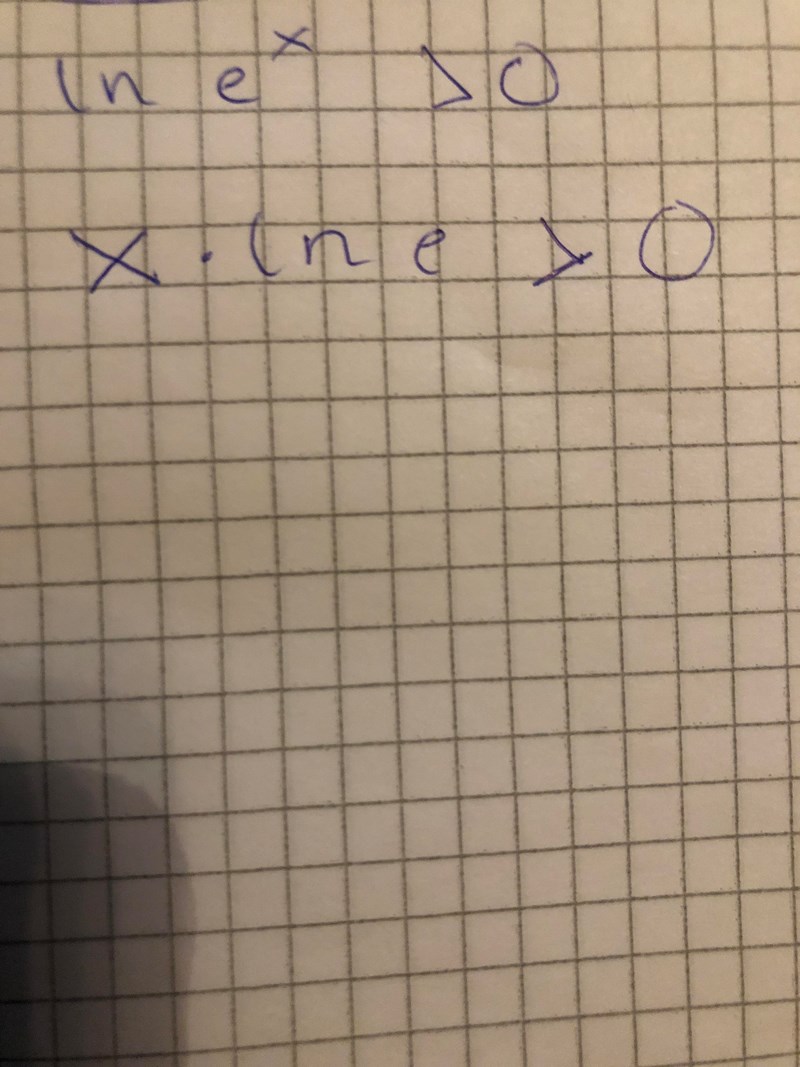 Blir ln e^x = x*ln (e) eller blir det ln e^x= x*ln e^x?
Blir ln e^x = x*ln (e) eller blir det ln e^x= x*ln e^x?
Det blr x*ln(e).
Och ln(e) = 1.
Så hela vänsterledet blir bara x.
Nen villkoret ska vara , inte >.
Bra, det var rätt svar på den ena frågan.
Hur långt har du kommit med den andra frågan?
f(x)= e^ x +x
f’(x)= e^x +1
f’(x) större eller lika med 0 (har inte tecknet ”större eller lika med på telefonen” men det är det jag menar när skriver >)
e^x + 1 > 0
e^x > -1
ln e^x > ln (-1)
x* ln (e^x) > ln (-1)
x > ln (-1)
verkar som att det inte är helt rätt för ln (-1) är odefinerat
Det stämmer.
Det betyder inte att olikheten saknar lösning utan tvärtom att olikheten är uppfylld för alla värden på .
Detta p.g.a. att termen för alla värden på , vilket innebär att flr alla värden på .
Tips: Du kan skriva som "a >= b" och som "a <= b"