Vilken funktion växer snabbast?

Denna fråga grundar sig i en uppgift som lyder "Bestäm gränsvärdet $\lim_{x \to \infty} \frac{3^{x}}{x^{3}}$ ." som förekommer i ma3. Resonemanget bör vara att en potensfunktion växer snabbare än en polynomfunktion och att gränsvärdet då skulle bli oändligheten. Detta är lätt att visa med ex. Geogebra:

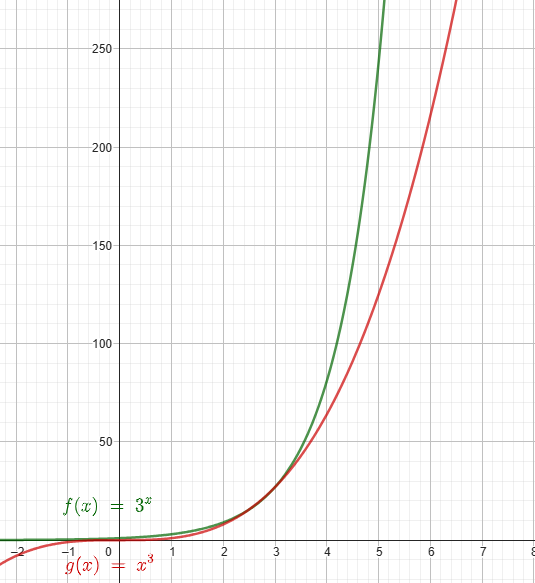
Säg att man ökar basen och exponenten till 10. I början växer 10^x snabbare, sedan går x¹⁰ om, men till sist inser man att 10^x ändå växer snabbast om x blir stort (se graferna nedan med olika skalning).

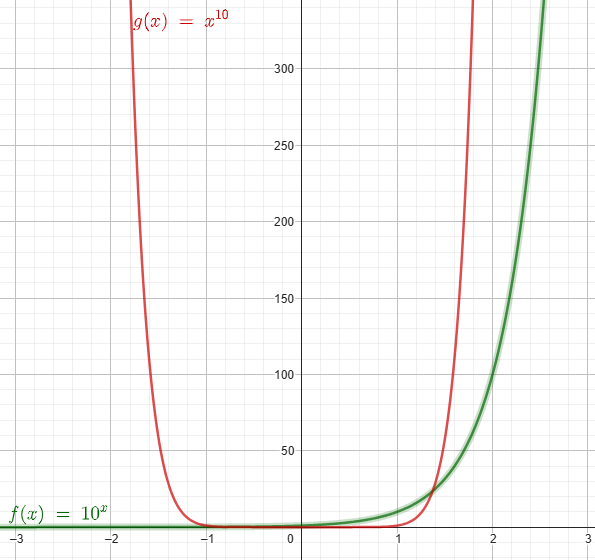
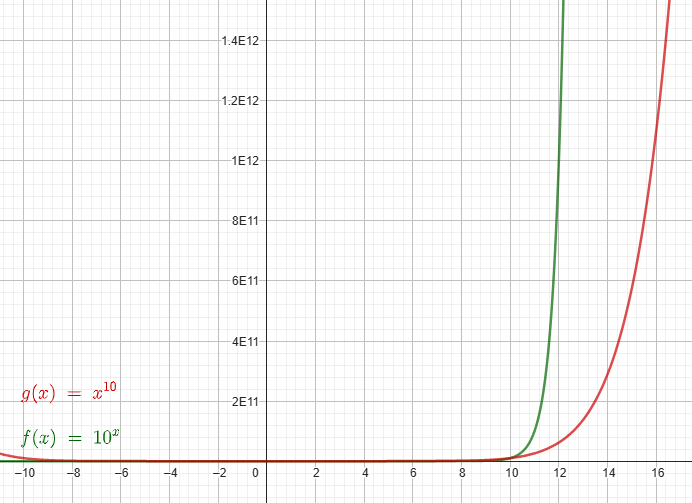
Frågan är nu om detta gäller även för x¹⁰⁰ och 100^x? Jag har zoomat ut så mycket som möjligt i y-led och det ser ju onekligen ut som att x¹⁰⁰ växer snabbare. Men finns det kanske en skärningspunkt långt där uppe i molnen där 100^x "går om" x¹⁰⁰? Isåfall, kan man hitta den?

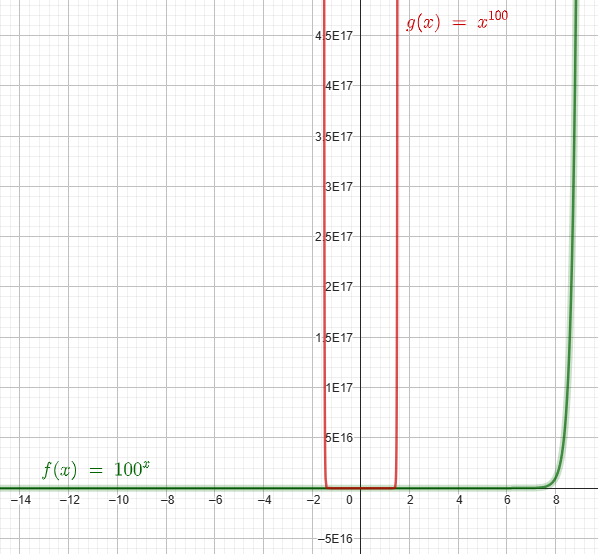
Det spelar faktiskt ingen roll vilket polynom du väljer, $x^{100}$ , $x^{100000}$ eller $x^{\text{googol}}$ eller $x^a$ där $a$ är vilket tal du vill; en exponentialfunktion kommer alltid att dominera i gränsvärdet.

Jag har inget formellt bevis på hand men man kan säkert föra något $\varepsilon$ , $\delta$ -resonemang. Men rent informellt är det väl ganska rimligt att ett tal upphöjt till oändligheten är större än oändligheten upphöjt till ett tal?

Tillägg: 27 okt 2025 12:02

De går väl om varandra vid $x=100$ ?

naytte skrev:
Det spelar faktiskt ingen roll vilket polynom du väljer, $x^{100}$ , $x^{100000}$ eller $x^{\text{googol}}$ eller $x^a$ där $a$ är vilket tal du vill; en exponentialfunktion kommer alltid att dominera i gränsvärdet.

Jag har inget formellt bevis på hand men man kan säkert föra något $\varepsilon$ , $\delta$ -resonemang. Men rent informellt är det väl ganska rimligt att ett tal upphöjt till oändligheten är större än oändligheten upphöjt till ett tal?

Tillägg: 27 okt 2025 12:02

De går väl om varandra vid $x=100$ ?

Jag tror det visas i Månsson, men jag har inte boken framför mig.

naytte skrev:
De går väl om varandra vid $x=100$ ?

Så måste det ju vara!

Jag har inget formellt bevis på hand men man kan säkert föra något ε,δ-resonemang.

Dessvärre lite komplicerat för en gymnasist, men tror jag kan övertyga en åk3:a mha mönstret i var de går om varandra :) Tack!

Om man kan utgå från att ln x är en växande funktion och att x>lnx så kan man jämföra logaritmerna.

Jag tittade i Månsson och beviset är tämligen tekniskt och gör vilken gymnasist som helst deprimerad (och ev. förtvivlad), så jag hoppar över det här. Vänta tills universitetet, då blir det mera "överkomligt".

Svara

Visa senaste svar