Vilket typ av tal är 0?

Låter bra. Det är även ett komplex tal, 0+0i.

Jag har på senare år glömt allt vad naturliga tal är. Jag finner inte beteckningen meningsfull, och definitionen varierar. Bättre säga "de positiva heltalen" för 1,2,3... och "icke-negativt heltal" för 0,1,2,... Då blir det aldrig tveksamheter IMO.

De relationerna du beskriver illustreras ofta med: 

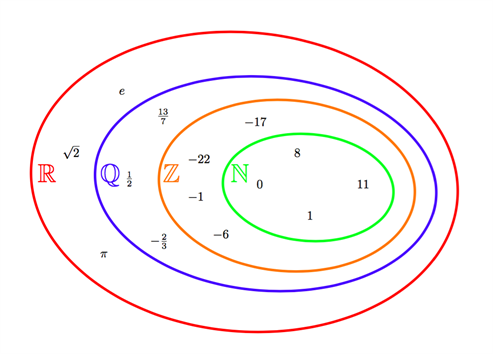
Här syns det tydligt att resonemanget du gör stämmer. 

En viktig sak jag bara vill nämna är att det enda valet du gör angående konvention är din punkt 1. Resterande slutsatser (punkt 2-4, att 0 är ett reellt tal, rationellt tal och ett heltal) är inget som styrs av konvention. Så är det alltid. 

Tack så mycket! Nu blev det genast klarare hur det ligger till. 

0 brukar räknas som ett naturligt tal. Om någon påstår att det inte är ett naturligt tal får du fråga hur han eller hon definierar sina tal...! :-)

Jag vet inte riktigt vilken nivå du ligger på matematiskt, men det kan vara värt att påpeka att nedanstående är en lite suspekt formulering:

Som jag har förstått är de reella talen ($\displaystyle \mathbb{R}$) en samling av alla tal utom de komplexa talen ($\displaystyle \mathbb{C}$) som är en utvidgning av de reella talen.

Man kan förutom $\mathbb{C}$ definiera (och använda!) många mängder till vilka $\mathbb{R}$ är en delmängd. Det som ska vara sagt är att $\mathbb{R}$ är en väldigt speciell mängd i många avseenden och har många fina egenskaper som andra mängder inte har och som vi ofta gärna vill använda (exempelvis supremumegenskapen som säger att varje icke-tommma, uppåt-begränsade delmängd till $\mathbb{R}$ har ett supremum i $\mathbb{R}$), men det finns många mycket "bredare" mängder än $\mathbb{R}$ också.

Man kan definiera vad man vill i matematiken!

naytte skrev:

Jag vet inte riktigt vilken nivå du ligger på matematiskt, men det kan vara värt att påpeka att nedanstående är en lite suspekt formulering:

Som jag har förstått är de reella talen ($\displaystyle \mathbb{R}$) en samling av alla tal utom de komplexa talen ($\displaystyle \mathbb{C}$) som är en utvidgning av de reella talen.

Man kan förutom $\mathbb{C}$ definiera (och använda!) många mängder till vilka $\mathbb{R}$ är en delmängd. Det som ska vara sagt är att $\mathbb{R}$ är en väldigt speciell mängd i många avseenden och har många fina egenskaper som andra mängder inte har och som vi ofta gärna vill använda (exempelvis supremumegenskapen som säger att varje icke-tom, uppåt-begränsad delmängd till $\mathbb{R}$ har ett supremum i $\mathbb{R}$), men det finns många mycket "bredare" mängder än $\mathbb{R}$ också.

Man kan definiera vad man vill i matematiken!

Jo, jag håller med dig. Jag vet inte heller vilken nivå jag ligger på rent matematiskt, men en sak är säker och det är att du och jag inte riktigt ligger på samma nivå (du är ju uppenbart betydligt mer insatt i alla detaljer än vad jag är!). Jag tycker det är ändå kul att läsa inlägg av personer som är djupt insatta i ett visst ämne eftersom motsatsen hade inte varit ett särskilt gott alternativ för mig... Nu när du nämner supremum måste jag erkänna att jag har hört talas om ordet och vet på ett ungefär vad det innebär rent begreppsmässigt, men det är inget jag använder i högre utsträckning. Jag har hört talas om supremum, infimum, majorant och minorant i mängdlära-sammanhang, men det är som sagt inte något jag använder dagligdags. Tyvärr...

Tack för att du tar upp det! Varje dag lär mig sig något nytt. :) 

Just supremumegenskapen är något man använder väldigt ofta i analys, om än implicit. Exempelvis förlitar du dig på den varje gång du integrerar (om jag inte tänker fel)!

naytte skrev:

0 brukar räknas som ett naturligt tal. Om någon påstår att det inte är ett naturligt tal får du fråga hur han eller hon definierar sina tal...! :-)

Det beror lite på tyvärr. Ibland räknar de in 0 i N, ibland inte. Det beror på land m.m. vad de anser vara 'korrekt' definition. 

Jag vet att anglosfären ofta envisas med det. Men hur definierar man sina tal om $0$ inte ligger i $\mathbb{N}$? I de vanliga konstruktionerna i ZF brukar ju $0$ vara det första talet man definierar (såvitt jag vet).

naytte skrev:

Jag vet att anglosfären ofta envisas med det. Men hur definierar man sina tal om $0$ inte ligger i $\mathbb{N}$? I de vanliga konstruktionerna i ZF brukar ju $0$ vara det första talet man definierar (såvitt jag vet).

Jag vet inte uppkomsten av N, kanske det berättar lite om varför (eller varför inte) 0 ingår. Om vi ser på alla dessa pysseluppgifter med mönster m.m. är det "naturligt" att tala om figur 1, 2, 3, ... och den har a_n "vad det nu är" symboler. 

För andra kan det vara "naturligt" att tala om att x_0 eller a_0 är ett startvärde och att a_1 är det första värdet därefter. 

Jag kan för lite om matematikhistoria.

De som tycker att N innehåller 0 brukar använda Z⁺ för de positiva heltalen.

naytte skrev:

Jag vet att anglosfären ofta envisas med det. Men hur definierar man sina tal om $0$ inte ligger i $\mathbb{N}$? I de vanliga konstruktionerna i ZF brukar ju $0$ vara det första talet man definierar (såvitt jag vet).

Man bara kallar det första talet man konstruerar för 1 och fortsätter som vanligt! Om man konstruerar heltalen som ekvivalensklasser av par av naturliga tal så kommer 0 att representeras av exempelvis (1,1), 1 av (2,1), 2 av ?(3,1) och så vidare. Ingen big deal, men det blir onekligen mer elegant om man har tillgång till 0 som ett naturligt tal.

Det kanske inte gör så stor skillnad, men jag blir lite fundersam kring hur man ska identifiera de naturliga talen med vissa heltal om vi inte får ha med noll som naturligt tal. Det typiska är ju att vi identifierar ett tal $a$ med ekvivalensklassen $[(a,0)]$ under $f:\mathbb{N}\to \mathbb{Z}$ som definieras av $f\left(n\right)=[(n,0)]$. Man visar att $f$ är 1-1 och ordningsbevarande och så är saken klar. Men man kanske lika gärna kan välja $f\left(n\right) = [(n+1,1)]$. Det blir inte lika snyggt men det kanske duger.

I ZFC är $0$ inte en godtycklig symbol utan den tomma mängden $\varnothing$. Eftersom $\omega$ definieras som den minsta induktiva mängden med egenskapen $\varnothing \in \omega$, kan man inte inom ramen för ZFC “flytta” $0$ från $\mathbb N$ till $\mathbb Z$ utan att ändra själva grunden för ordning, ordinaler, rekursion och induktion.

Visst kan man hävda att $\mathbb{N}$ inte måste följa ur ZFC och det går att visa att en icke-standard-Peanomodell med första element 1 är isomorf till ZFC-standard $\mathbb{N}$, men ordinalmodellen i ZFC kan inte reduceras till en simpel Peano-modell utan förlust av centrala egenskaper vi använder i andra delar av matematiken såsom transfinit rekursion, Replacement (ersättningsaxiomet), gruppkonstruktioner och den systematiska behandlingen av ordinaler och kardinaler.

Att $0\in \mathbb{N}$ är alltså inte en konvention utan en strukturell konsekvens av ZFC, och att utesluta $0$ medför betydande teoretiska nackdelar utan motsvarande strukturella vinster. De få matematiska skäl som anförs för motsatsen är i huvudsak tillämpnings- och kontextberoende och saknar därmed relevans för den mängdteoretiska grundkonstruktionen.

@D4NIEL: Kan du ge något mer konkret exempel på de betydande teoretiska nackdelar du har i åtanke?

Jag ser t.ex. inte riktigt hur nollan som naturligt tal är så speciellt fundamentalt för transfinit rekursion, eller har någon omedelbar koppling till ersättningsaxiomet? Jag är heller inte riktigt med på vad begreppet gruppkonstruktioner syftar på i det här sammanhanget.

naytte skrev:

Men man kanske lika gärna kan välja $f\left(n\right) = [(n+1,1)]$. Det blir inte lika snyggt men det kanske duger.

Japp, det är precis det jag menar. Och ja, det blir lite fult, men i slutändan kommer du få samma (upp till isomforfi) heltal, rationella, reella tal, komplexa tal och så vidare. Så just när det kommer till talkonstruktioner så tror jag inte det spelar någon roll om det första naturliga talet är 0 eller 1.

Däremot kanske det finns det något mer fundamentalt problem i stil med der D4NIEL verkar vara inne på. Jag hoppas att han eller någon annan som kan mer mängdlära än mig kan utveckla resonemanget lite! 

Väntar också ivrigt på vidare diskussion! Låter väldigt intressant. 

Orsaken till att man kan betrakta 0 som ett icke-naturligt tal skulle jag säga har att göra med i vilken ordning man hittade på/upptäckte talen. En historia som jag har på känn kan vara helfel och bara vara något jag fått för mig, så jag välkomnar om folk rättar mig:

Första räkningen man gjorde var att man hade en viss mängd av något och lade till en annan mängd av samma något och fick fram en ny mängd. Att man sedan insåg att detta gällde oavsett vad detta "något" må vara och att resultatet var bestående och att man fick samma resultat även om man gjorde andra ordningar eller tog bitar av ena mängden till den andra innan man adderade är orsaken till att matematiken är så stark: den är ofta gångbar. Så med detta kunde man bilda alla hela mängder, något de gamla grekerna i tur och ordning kallade alfa, beta, gamma, osv, som vi kallar ett, två, tre osv. Teoretiskt oändligt stor mängd.

Sedan insåg man efter ett tag att man även vill kunna undersöka vad som händer då man tar bort mängder från mängder. Man upptäckte då att det fanns en hel hoper mängder som man missat, men om man lade till dem till de kända mängderna gjorde man matematiken mer komplett och gångbar, och applicerbar i fler tillfällen. Med de nya mängderna eller talen fick man heltalen.

Sedan insåg man att man ibland ville kunna addera samma mängd ett visst antal gånger, och därvidlag upptäckte man att man inte fick några nya mängder från detta. Då man däremot vände på steken och frågade "vilken mängd måste jag ta ett visst antal gånger för att få den här mängden?" upptäckte man division och att det fanns ytterligare mängder som man tidigare missat. Med dessa nya tal hade man de rationella talen, kvottalen.

Sedan försökte man mäta andra förhållanden och insåg att det förfarandesätt man ville använda sig av inte gav ett tal som kunde uttryckas komplett som en kvot (t.ex. vilket tal gånger sig självt blir det här talet; vad är förhållandet mellan en cirkels omkrets och dess diameter), och därmed fick man expandera med alla dessa till att bilda de reella talen.

Därefter försökte man ta till sin roten-ur-operation på de negativa talen, insåg att om man hittar på talet i så får man en mer komplett och mer applicerbar matematik, trots att Lewis Carroll tyckte det var helt upp-och-ner, och bildade därmed de komplexa talen.

Om man har ovanstående synsätt skulle det innebära att nollan först uppkommer då man får för sig att subtrahera en mängd med sig själv, dvs. vid bildandet av heltalen. Man kan hävda att man borde känt till den från första början, som en del av de naturliga talen. Men då drar jag mig till minnes att år 0 aldrig existerat. Så trots att vi idag kan tycka att det ter sig en självklarhet att ha med nollan som de mest naturliga talen så är det en konstruktion som bara ter sig så eftersom vi sitter med facit i hand och är väl bevandrade med konceptet. Därmed är det rimligt att låta nollan ingå i heltalen men ej de naturliga talen.