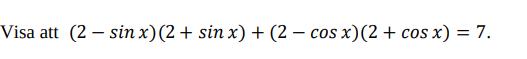Visa att (2 - sin x)(2 + sin x ) + (2 - cos x )(2+cos x ) = 7

ii_noor06 skrev:

Behöver hjälp... svara inte mig till jag själv försöker göra uppgiften!

Börja med att använda konjugatregeln två gånger.

Jag gjorde så här..

( 2 - sin x ) ( 2 + sin x ) + ( 2 - cos x ) ( 2 + cos x )

( 2 - sin x ) ( 2 + sin x ) = 2 * 2 +  2 sin x  -  2 * sin x = 4 

( 2 - cos x ) ( 2 + cos x ) = 2 * 2 +  2 *cos x  -  2 * cos x = 4

Fel vet men det var så jag förstod konjugatregeln

sin(x)^.sin(x) är inte lika med 2 sin(x), utan sin²(x), och på samma sätt med cosinus.

Smaragdalena skrev:

sin(x)sin(x) är inte lika med 2 sin(x), utan sin²(x), och på samma sätt med cosinus.

Vart står det sin(x)sin(x)

Tillägg: 17 jan 2024 15:32

( 2 - sin x ) ( 2 + sin x ) = 2 * 2 +  sin²(x) - sin²(x) = ?

( 2 - cos x ) ( 2 + cos x ) = 2 * 2 +  cos²(x) -  cos²(x) = ?

Så?

ii_noor06 skrev:

Jag gjorde så här..

( 2 - sin x ) ( 2 + sin x ) + ( 2 - cos x ) ( 2 + cos x )

( 2 - sin x ) ( 2 + sin x ) = 2 * 2 +  2 sin x  -  2 * sin x = 4 

( 2 - cos x ) ( 2 + cos x ) = 2 * 2 +  2 *cos x  -  2 * cos x = 4

Fel vet men det var så jag förstod konjugatregeln

Och då blir det fel. Om vi räknar med färgläggning:

$$\begin{gathered} \left(2-\sin \left(x\right)\right)\left(2+\sin \left(x\right)\right)= \\ \left(2-\sin \left(x\right)\right)\left(2+sin\left(x\right)\right)= \\ 2*\left(2+sin\left(x\right)\right)-\sin \left(x\right)*\left(2+sin\left(x\right)\right)= \\ 2*\left(2+sin\left(x\right)\right)-\sin \left(x\right)*\left(2+sin\left(x\right)\right)= \\ 2*2+2*sin\left(x\right)-\sin \left(x\right)*2-\sin \left(x\right)*sin\left(x\right)= \\ 2*2+2*sin\left(x\right)-sin\left(x\right)*2-sin\left(x\right)*sin\left(x\right)= \\ {2}^2+2*sin\left(x\right)-sin\left(x\right)*2-{\sin \left(x\right)}^2= \\ {2}^2+\cancel{2*\sin \left(x\right)}-\cancel{\sin \left(x\right)*2}-{\sin \left(x\right)}^2= \\ {2}^2-{\sin \left(x\right)}^2 \end{gathered}$$

Eller som en av kvadreringsreglerna säger:

$\left(a+b\right)*\left(a-b\right)=a^2-b^2$

där nu a är 2 och b är sin(x).

Tack för din tydliga lösning...men hur visar jag då att det blir lika med 7?

Använd samma kvadreringsregel för de två produkterna och se vad som händer.

Bedinsis skrev:

Använd samma kvadreringsregel för de två produkterna och se vad som händer.

$$\begin{gathered} ( 2 - \cos ( x ) ) ( 2+\cos ( x ) )= \\ ( 2 - \cos ( x ) ) ( 2 + cos ( x ) )= \\ 2 * ( 2 + cos ( x ) ) - \cos ( x ) * ( 2 + cos ( x ) )= \\ 2 * ( 2 + cos ( x ) ) - \cos ( x ) * ( 2+cos ( x ) ) = \\ 2 * 2 + 2 * cos ( x ) - \cos ( x ) * 2 -\cos ( x ) * cos ( x )= \\ 2 * 2 + 2 * cos ( x ) - cos ( x ) * 2 -cos ( x ) * cos ( x )= \\ {2}^2+ 2* \cos ( x ) - \cos ( x ) * 2 -\cos {( x )}^{2 }= \\ {2}^2- \cos {( x )}^2 \end{gathered}$$

Rätt?

Rätt, men den normala beteckningen är cos²(x). Sätt nu ihop de båda halvorna och förenkla.

Det är det, men kvadreringsregeln som jag skrev sist är till för att man inte skall behöva skriva ut alla de där stegen; egentligen räcker det med första och sista raden i ditt inlägg.

Jag skrev mest steg för steg för att vara pedagogisk och lära ut.

Det Smaragdalena sade stämmer även.

Det är det, men kvadreringsregeln som jag skrev sist är till för att man inte skall behöva skriva ut alla de där stegen; egentligen räcker det med första och sista raden i ditt inlägg.

Hur är det man gör med kvadreringsregeln...?

Smaragdalena skrev:

Rätt, men den normala beteckningen är cos²(x). Sätt nu ihop de båda halvorna och förenkla.

sin²(x)+cos²(x),

Rätt?

Vart tog 2²:orna vägen?

Bedinsis skrev:

Vart tog 2²:orna vägen?

2² sin²(x)+ 2² cos²(x),

Nu är det rätt, glömde bort de 

Vart tog minustecknen vägen?

Bedinsis skrev:

Vart tog minustecknen vägen?

Hahaha... jag är helt slut alltså,

2² - sin² ( x ) + 2² - cos ² ( x )

Nu rätt?

Det borde det vara.

Nu ska jag förkorta,

2² - sin² ( x ) + 2² - cos ² ( x ) =

2*2 - sin² ( x ) + 2 * 2 - cos² ( x ) = 

4 - sin² ( x ) + 4 - cos ² ( x ) =

sin² ( x ) - cos² (x ) =

Vad ska jag göra sen?

Du har tappat bort ett viktigt minustecken. När du har hittat det, kan dui använda trigonometriska ettan.

Jag hittade faktiskt inte den, glömde jag bort den från min uträckning eller vart?

På näst sista raden börjar det 4-sin²(x), på sista raden har minustecknet försvunnit. Dessutom har du fått 4+4 att bli 0, inte 8.

Smaragdalena skrev:

På näst sista raden börjar det 4-sin²(x), på sista raden har minustecknet försvunnit.

Ja för det finns ett +4 och -+ tar ut varandra så inget blir kvar eller har jag fel?

Tillägg: 17 jan 2024 17:24

aha blir det så här då,

-sin² ( x ) - cos² (x ) + 8 

Jadå.

Trigonometriska ettan är nästa steg.

Bedinsis skrev:

Jadå.

Trigonometriska ettan är nästa steg.

Förlåt men vad är trigonometriska ettan?

Trigonometriska ettan anger förhållandet mellan sin²x och cos²x:

$\displaystyle \sin^2x+\cos^2x=1$

Du kan använda det förhållandet om du gör omskrivningen:

$\displaystyle -\sin^2x-\cos^2x+8=-(\sin^2x+\cos^2x)+8$

naytte skrev:

Trigonometriska ettan anger förhållandet mellan sin²x och cos²x:

$\displaystyle \sin^2x+\cos^2x=1$

aha

Tillägg: 17 jan 2024 17:31

Vänta ska testa räkna ut det

$$\begin{gathered} -sin²\left(x\right)-cos²\left(x\right)+8 = \\ 8-1(\sin ²x+\cos ²x) = \\ 8 - \left(1\right) = \\ 8- 1*1 = \\ 8-1 = \\ 7 \end{gathered}$$

.

Är det rätt eller?

Ja.