Visa att |z * w| = |z|*|w| och |z/w| = |z|/|w|
Hejsan, allihopa.
Jag har några funderingar kring facits lösningar till dessa två uppgifter:
Visa att
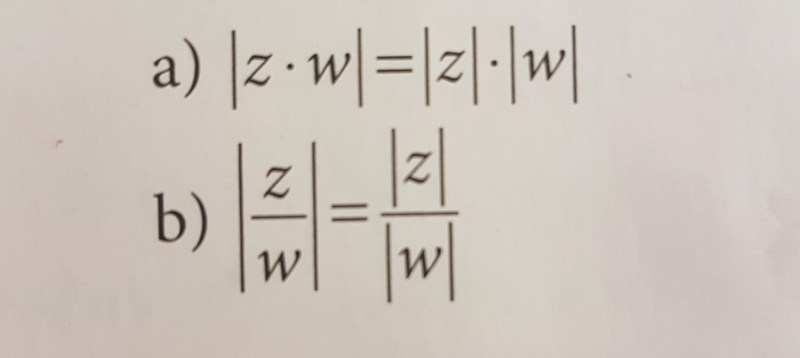
Stegen som jag ej förstår har pilar riktade mot sig.
a):
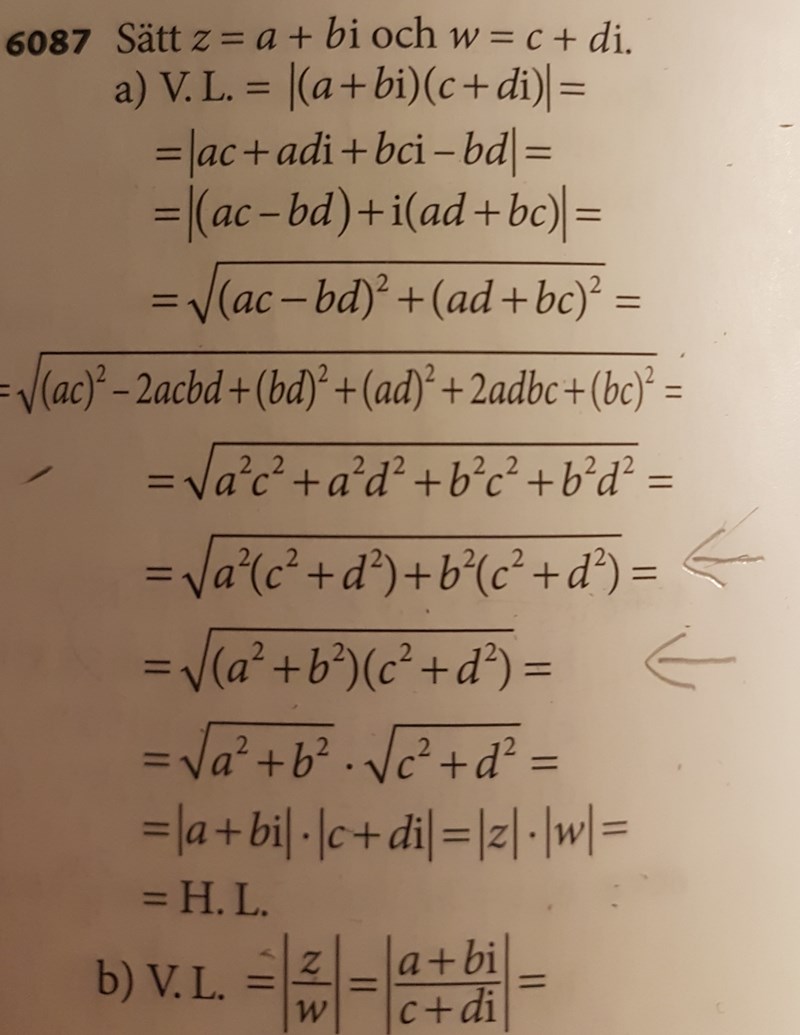
b):
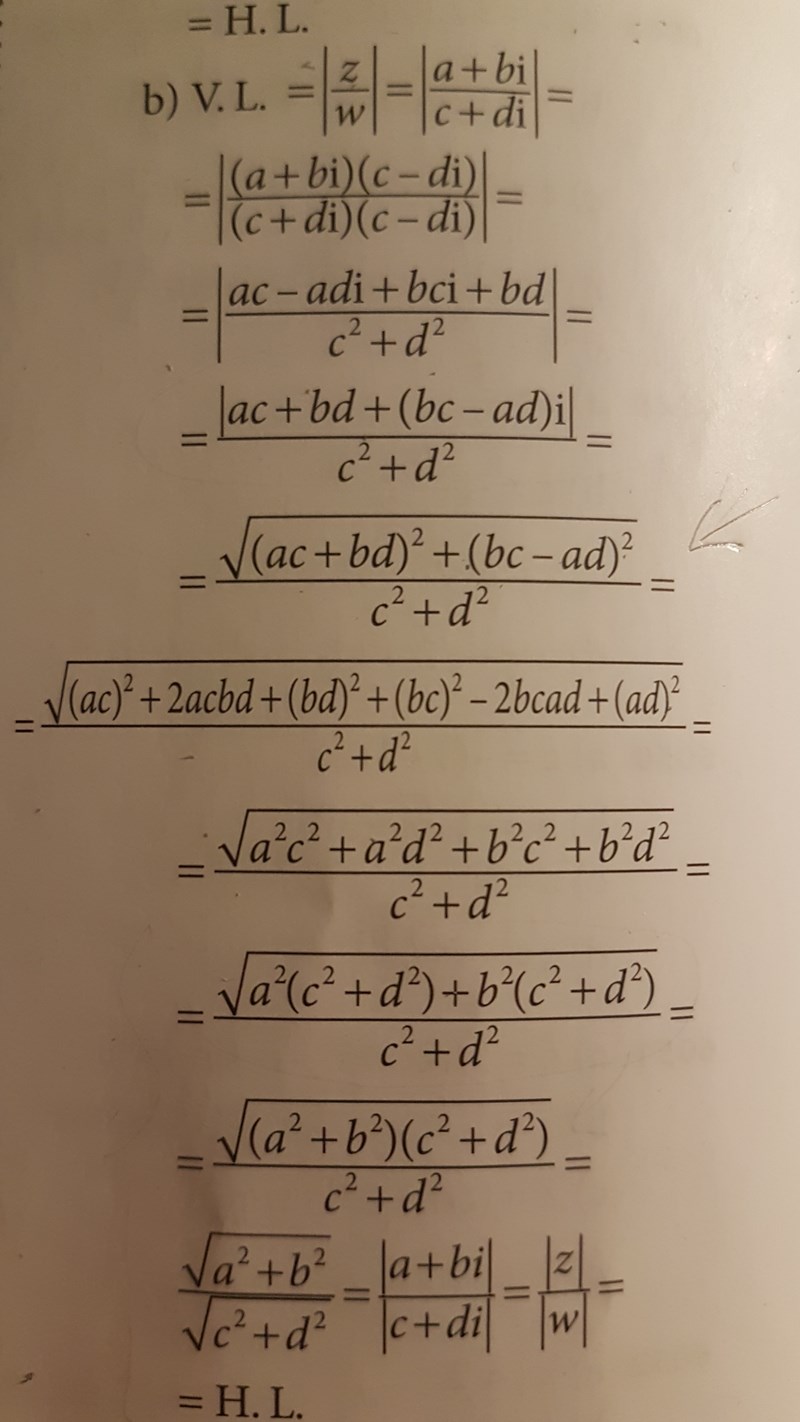
På a) vet jag inte hur √(a²(c² + d²) + b²(c² + d²)) = √((a² + b²)(c² + d²)). Och på b) vet jag ej varför man utrycker täljaren som ett absolutbelopp men låter nämnaren vara.
Tack
Hej,
Uppgift a. Hos termerna i summan är faktorn gemensam och kan därför (via den så kallade distributiva lagen) brytas ut för att ge de önskade resultatet.
Uppgift b. Täljaren är absolutbeloppet av ett komplext tal medan nämnaren är ett positivt reellt tal och behöver därför inget absolutbelopp.
Ett alternativt sätt baseras på att absolutbelopp för komplext tal kan uttryckas via konjugatet
Då kan man skriva följande.
Ta kvadratrot och kom ihåg att absolutbelopp aldrig är negativa för att få
Tack så hemskt mycket :)

