Vridmoment planka
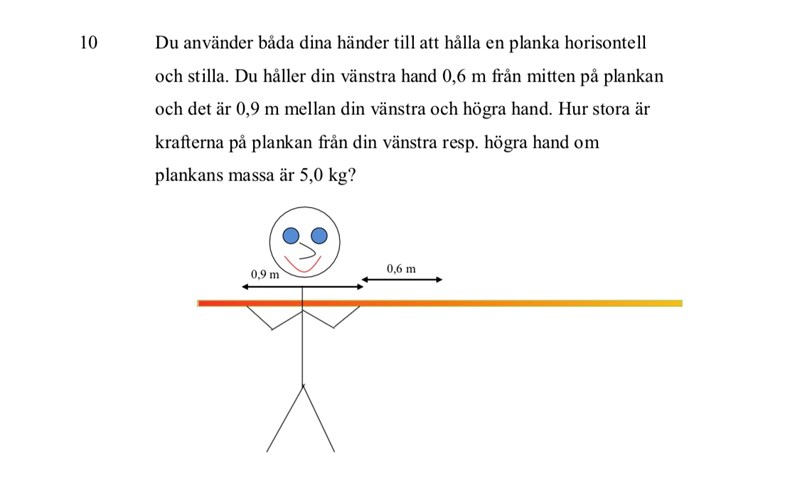
Har problem med denna uppgift.
högerhand (F1) vänsterhand (F2)
F1•0,9+F2•0,6=mg (3-1,5)
vet inte om det är korrekt ens men vet inte hur jag ska tänka när jag ska lösa ut F i vardera hand..
Börja alltid med att rita en figur, där krafterna och deras riktningar syns tydligt. Enklast är sedan att räkna momentjämvikt runt en av krafternas angreppspunkter, till exempel från högerhanden: 1,5 mg - 0,9 F2 = 0. Eller från vänsterhanden: 0,6 mg - 0,9 F1 = 0.
jag förstod ikte riktigt. Både F2 och F1 är riktade upp och mg ner.
Hur kan mg(1,5) inte behöva användas när jag ska räkna ut F1?
Du kan välja vilken rotationspunkt du vill på plankan och räkna med moment-jämvikt. Men att välja en av händerna som rotationspunkt gör att du får en ekvation med enbart en obekant. Därmed är det enkelt att räkna ut den kraften. Sedan räknar du ut den andra kraften utifrån att summan av alla krafter är noll.
Men viktigast för att det ska bli enkelt att göra rätt är att rita en korrekt figur.
Tips: rita personen bakifrån, så att högerhanden är åt höger. Det minskar risken att man gör fel (åtminstone skulle risken för MIG att göra fel på höger och vänster vara överhängande, om jag skulle rita situationen framifrån).
Okej så om vi ritar den såhär istället har vi höger närmast mitten och momentpunkt på höger hand.
F2 Blir då alltså F2•0,9=mg•1,5
F1 känns inte lika logiskt att det ska bli mg•0,6=0,9•F1?
Hur kan r bli olika på F1 och F2?
När du ritar det så och väljer högerhanden som momentpunkt blir momentjämviktsekvationen 0,6 mg + 0,9 F1 = 0. Båda krafterna ser i figuren ut att ge en rotation medsols. Men när du löser ut F1 ser du att den blir negativ, alltså riktad åt andra hållet egentligen.
Ja då blev ju kraften negativ....
men varför kan man inte räkna F1•0,9=mg•0,6 om jag ritar såhär?
Och F2: F2•0,9=mg•1,5 F2=82N. Fast F2 ska vara nedåt. Alltså negativ.
För att krafter och moment har riktningar, och du måste bestämma dig för vad som är positiv riktning, till exempel att krafter uppåt ger plustecken, krafter neråt minustecken, moment medsols plustecken, moment motsols minustecken. I enkla uppgifter kan man förstås, som du gör, tänka så det blir rätt, men ganska snart blir det ändå fel om man inte håller stenhårt på riktningar och tecken.
Men om jag löser F2: F2•0,9+mg•1,5=0 blir svaret rätt? Men man kanske inte får göra så då?
Det blir alltså inte rätt, för det stämmer inte med riktningen du har angett för F2 i figuren. Med din uträkning av F2, där den blir negativ, skulle den bli riktad neråt, vilket den inte är.
En kraft ska vara riktad nedåt enl facit med 82N. Blkr det F1 i detta fall jag målat då?
Du bör kunna se, om du tänker efter, hur krafterna är riktade (kom ihåg att det är krafterna som verkar på plankan det gäller).
Annars, om du följer figuren och gör rätt med tecken, så får du ut riktningen i beräkningen. Negativ kraft betyder att riktningen är motsatt den du antagit i figuren.
Om jag ska räkna ut F2 enl min bild tänker jag F1 mot och mg med
Jag förutsätter att figuren i början är given med frågan?
Vi behåller dina definitioner av = höger hand och = vänster hand.
Jag lägger till en definition för plankans kraft.
Vad kommer att hända? Plankan vill vridas medurs runt rotationspunkt vänster hand.
Höger hand måste hålla emot med en nedåtriktad kraft
Då får vi vilket är samma sak som HT-Borås skrev
Ser du det? Alltså att höger hand måste hålla emot exakt så mycket som plankans kraft ger.
Då kan du lösa ut
Sist så adderar du de två krafter som trycker nedåt och då får du en summa kraft nedåt som
vänster hand måste motverka, men viktigt att tänka är att det hade kunnat vara ett stöd där istället. Vad händer i den punkten?
Från ett stöd får man en normalkraft riktad uppåt och det är vad vänster hand i detta fall utför.
