Andragradsfunktioner
Hej, skulle behöva hjälp med den här uppgiften om någon kan hjälpa mig?
Beräkna symmetrilinjen och vändpunkten för (8+2x)(5−x)
Jag har försökt kolla i böcker, nätet, tagit hjälp av andra. men jag förstår fortfarande noll!
Tack på förhand!
Välkommen till Pluggakuten! Först och främst behöver du utveckla funktionsuttrycket. kan utvecklas till att ha formen av en klassisk andragradsfunktion. Detta gör du genom att multiplicera varje term i den ena parentesen, med alla termer i den andra parentesen. Vad får du då för funktionsuttryck?
Tack! Så då menar du att jag måste ta 8 * 5 och 8 * X och sen 2x * 5 och 2x * x?
Och då få svaret 8*5=40, 8*x=8x och 2x*5=10x och 2x*x=2x?
Eller tänker jag helt fel?
Josefinebrolund skrev:Hej, skulle behöva hjälp med den här uppgiften om någon kan hjälpa mig?
Beräkna symmetrilinjen och vändpunkten för (8+2x)(5−x)
Jag har försökt kolla i böcker, nätet, tagit hjälp av andra. men jag förstår fortfarande noll!
Tack på förhand!
Hej.
Uttrycket (8+2x)(5-x) är ett (faktoriserat) andragradsuttryck. De två faktorerna är (8+2x) och (5-x).
Funktionen y = (8+2x)(5-x) är en andragradsfunktion.
Grafen till en andragradsfunktion är symmetrisk kring symmetrilinjen.
Symmetrilinjen ligger mitt emellan funktionens nollställen.
Eftersom andragradsuttrycket redan är faktoriserat så kan du enkelt hitta uttryckets nollställen med hjälp av nollproduktmetoden.
Det ena nollstället fås då ena faktorn är lika med 0 och det andra nollstället fås då den andra faktorn är lika med 0.
Symmetrilinjen ligher som sagt mitt emellan dessa nollställen och uttryckets vändpunkt (extremvärde) ligger på symmetrilinjen.
Så då menar du att jag ska ta 8+2x=0 och 5-x=0 så jag får fram vad x är och sen behöver jag göra en graf för att få fram symmertrilinjen och vändpunkten?
Ja, det är ett annat sätt att göra det. Kör på Yngves sätt, det är nog lättast. Vilka är funktionens nollställen? Vilket x-värde har symmetrilinjen?
Förlåt, den här uppgiften är verkligen supersvår när man inte jobbat med det innan, men då börjar jag med att ta 8+2x=0 och 5-x=0 för att få fram vad x:et är till att börja med, eller är jag helt vilse?
Ja, du vill hitta de två nollställena till funktionen, och dessa hittas genom att lösa de ekvationer du skrivit.
Nu har jag fått fram svaren
x1 = -4
x2 = 5
Ska jag nu göra en graf där -4 och 5 ligger på x axeln och när jag ritat ut alla siffror kolla om vändpunkten är minimipunkt eller en maximipunkt? Och då ser jag även vart symmetrilinjen går?
Bra! Använd dig nu av att extrempunkten (vändpunkten) hos en andragradsfunktion alltid ligger mittemellan nollställena. Vilket x-värde har extrempunkten? Vilket y-värde får du om du stoppar in det värdet i f(x)?
Läs tillbaka lite i tråden.
En viktig slutsats är att symmetrilinjen ligger mitt emellan nollställena på en andragradsfunktion/graf. Då bör du försöka konstatera vilket x-värde som ligger mitt emellan x=-4 och x=5. Hur kan du göra detta?
Maximi/minimi-punkten där kurvan vänder kommer sedan ligga på symmetrilinjen.
Så börja därför i änden med att bestämma symmetrilinjen.
(Edit: Smutstvätt hann före, jag tänkte ju att jag skulle avlasta dig lite Smutsis, eftersom du säkert har fullt upp att svara på mina PM ;) ).
Jag ritade upp en graf med en y och x axel och placerade sedan ut -4 ända bort till 5 på x axeln och räknade sedan ut vart mitten är, och där borde även symmetrilinjen ligga, så om jag har förstått det rätt så borde symmetrilinjen ligga på 1 och vändpunkten ligger också på ett och är maximi.
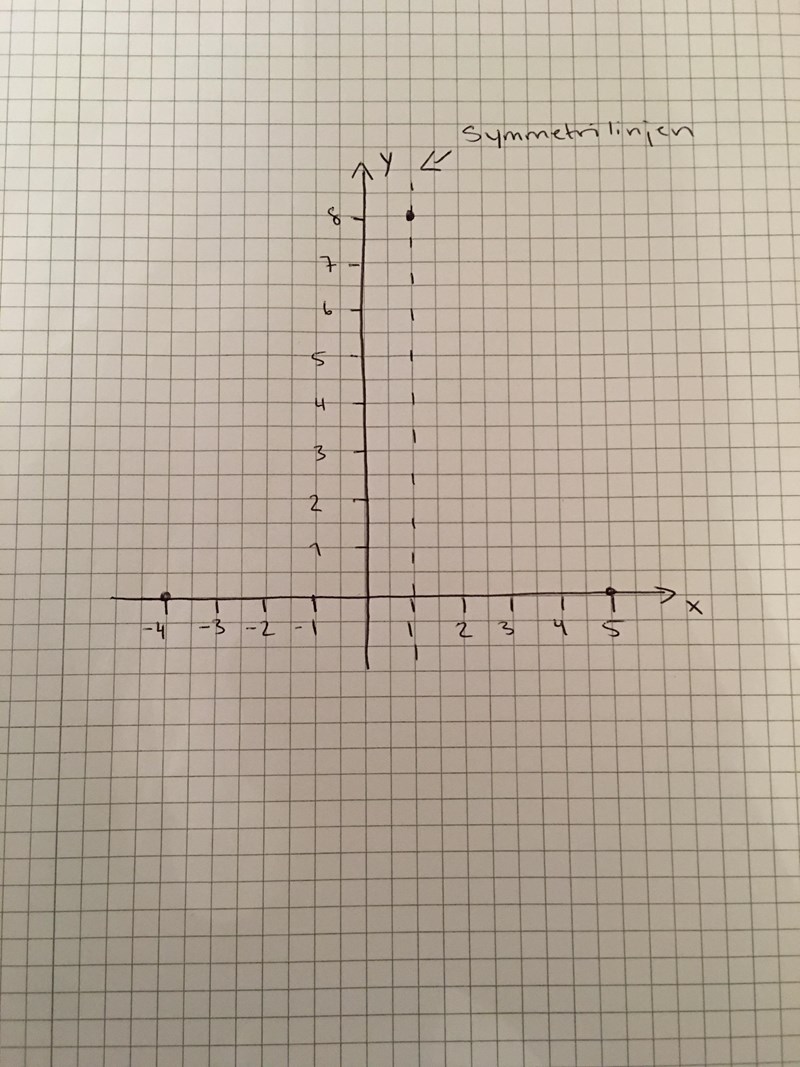
1 ligger inte mitt emellan -4 och 5 (det är 5 steg mellan -4 och 1 men bara 4 steg mellan 1 och 5).
Då är det jag som räknat fel och symmetrilinjen borde hamna på 0,5 för då är det 4,5 från -4 och 4,5 från 5?
Så symmetrilinjen är 0,5 och vändpunkten samma och är maximi? Tack snälla för all hjälp!!
En punkt består av två koordinater (x,y) , alltså en x-koordinat och en y-koordinat. Du vet att extrempunkten ligger på linjen x=0,5. Hur kan du ta reda på punktens y-koordinat alltså y-värdet när x=0,5?
Hur har du kommit fram till att det är en maximipunkt?
Jag antog att y-värdet va 8, då det såg ut såhär när jag dragit parabelen. och maximipunkten kom jag fram till när jag även där drog parabelen. 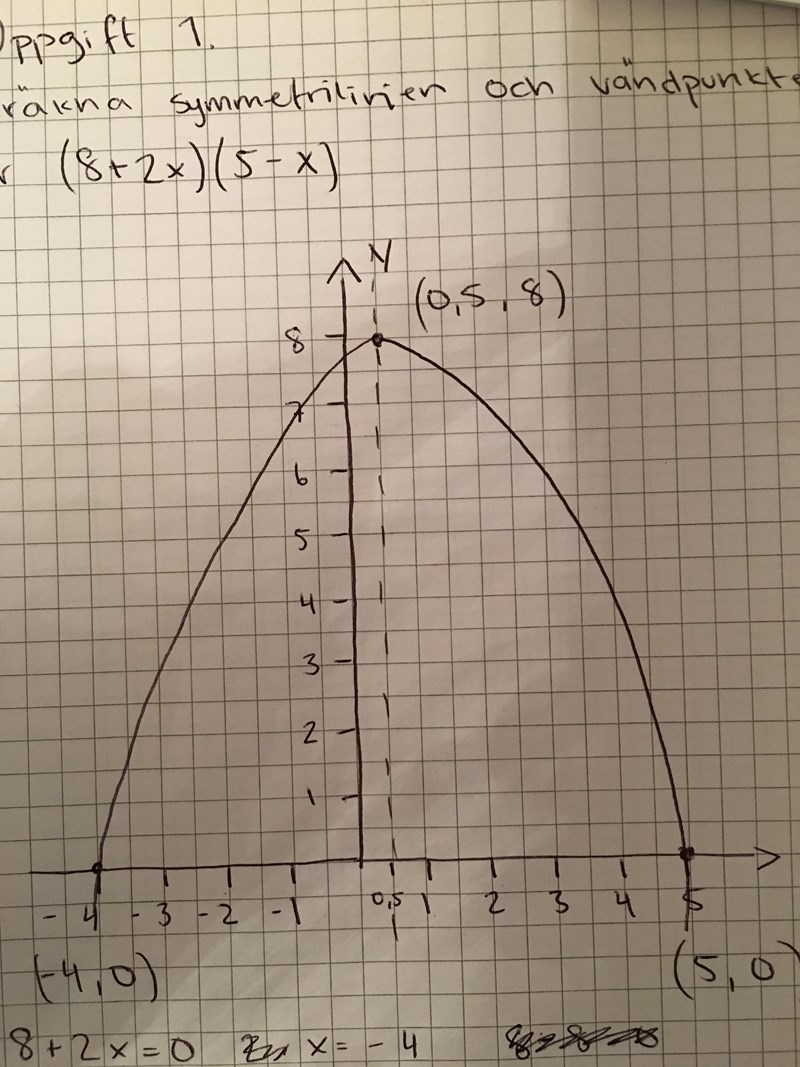
Hur fick du fram att y(0,5)=8?
Nu känner jag mig ganska vilsen och vet inte alls vad jag ska göra efter att jag kom fram till att symmetrilinjen är 0,5. Ska jag nu ta reda på vilka alla v-koordinater är?
Du skall börja med att stoppa in värdet funktionen . Vad får du för y-värde?
Du behöver få ut koordinaterna för vändpunkten. Den ligger på symmetrilinjen således är x-kordinaten för denna punkt x=0,5
. Du behöver ta reda på y-kordinaten nu också, den är också en del av punkten.
Du kan inte bara anta. Hur vet du vad funktionens y-värde är när x=0,5? Detta har du säkert gjort förut.
Har man ritat grafen bra, så kan man såklart läsa ut det ur grafen
8+2*0,5*5-0,5=40,5
kan det stämma, då är alltså funktionen y = 40,5?
Ja uträkningen ser ut att stämma. Men du söker inte en funktion, du söker en punkt.
(Extrem)punkten är alltså (
Om du tänkt till och ritat grafen korrekt, så kan du av denna se om denna blir en maximipunkt eller minimipunkt.
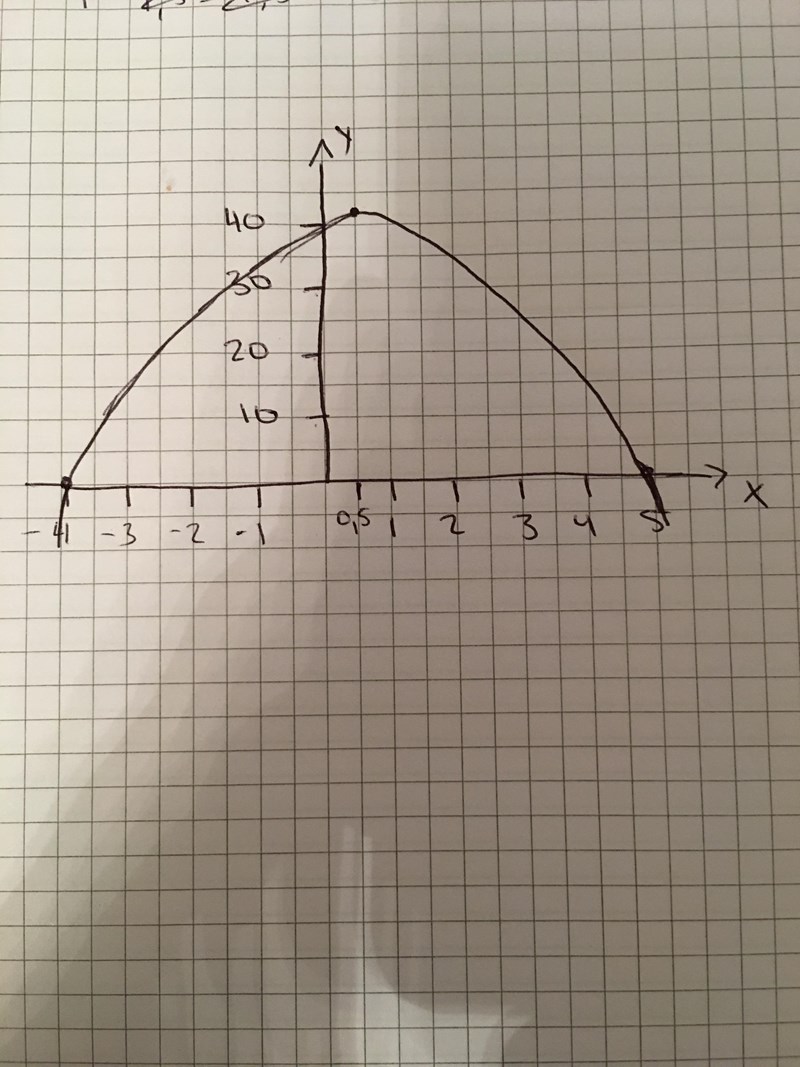
Om jag nu har ritat grafen rätt, så ser jag att grafen är öppen nedåt, då borde det betyda det blir en maximipunkt? Eller?
Din andragradskurva är lite för spetsig, den borde se ut så här i stället, mendu har alldeles rätt i att det är en maximipunkt.
Så att jag är helt med nu så är symmetrilinjen 0,5 och vändpunkten är 40,5 och det är en maximipunkt för att grafen är öppen nedåt? :)
Ja, symmetrilinjen är x=0,5 (inte bara 0,5) men vändpunkten har två koordinater - det är en maximipunkt som har koordinaterna (0,5;40,5). Du ser att det är en maximipunkt eftersom funktionen har sitt maximala (= största) värde där.
Josefinebrolund skrev:Så att jag är helt med nu så är symmetrilinjen 0,5 och vändpunkten är 40,5 och det är en maximipunkt för att grafen är öppen nedåt? :)
Nej 0,5 är ett tal, ingen linje. Däremot är x = 0,5 en linje, nämligen den vertikala streckade linjen som du ritat i ditt koordinatsystem.
Rätt svar är alltså att symmetrilinjen är x = 0,5.
På samma sätt så är 40,5 ett tal, ingen punkt. En punkt har både x- och y-koordinat. I detta fallet x-koordinaten 0,5 och y-koordinaten 40,5.
Rätt svar är alltså att vändpunkten är (0,5; 40,5)
Aha, jag fattar!! Tack snälla för all hjälp och för att ni har tagit er tid att hjälpa mig! Det uppskattas verkligen! :)
Josefinebrolund skrev:Aha, jag fattar!! Tack snälla för all hjälp och för att ni har tagit er tid att hjälpa mig! Det uppskattas verkligen! :)
Vsg. Läs gärna igenom förklaringarna av de viktiga begreppen här.





