Antiderivatan / Primitiv funktion
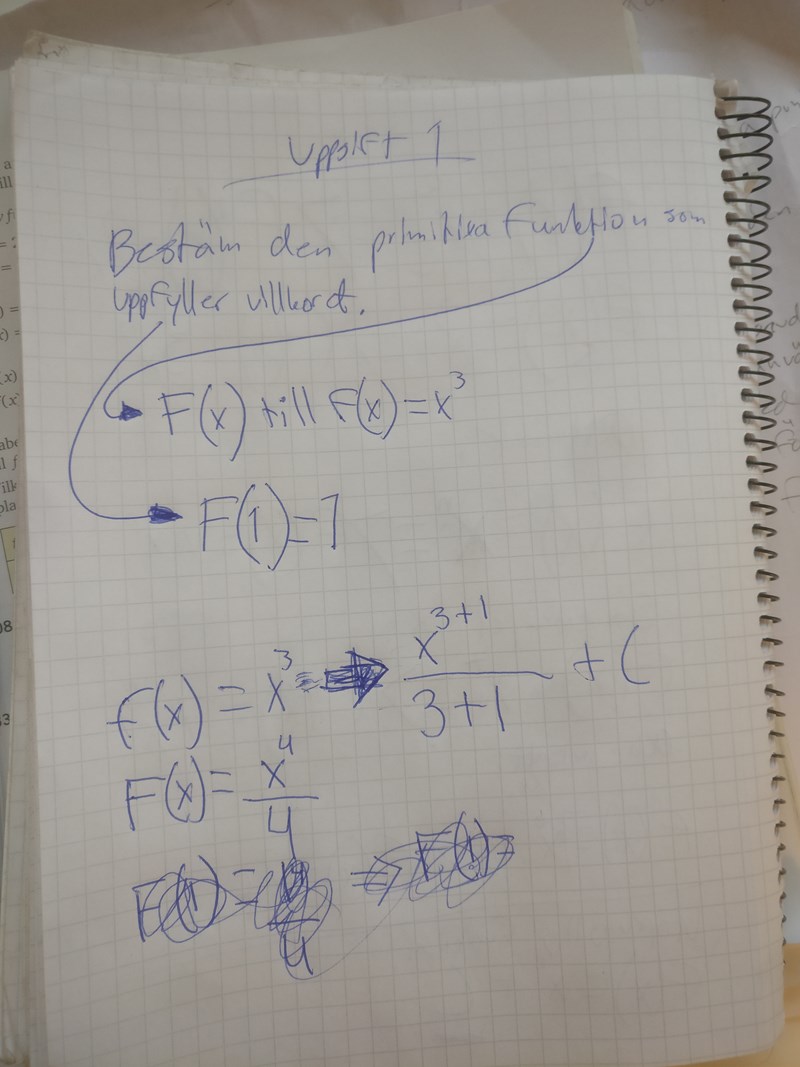
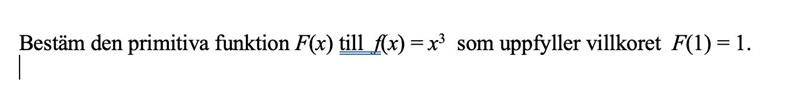
Hej!
Jag tror jag förstår grundkonceptet kring primitiva funktioner och antiderivatan, men jag har lite svårt att tolka vad uppgiften frågar efter.
Och sen är det lite oklart vad reglerna är runt att "antiderivera" när talet är t.ex eftersom derivatan av det är . Då blir det ju liksom en "vanlig" derivata.
Antiderivata är inte ett helt korrekt ord, men det är praktiskt och beskriver precis vad en primitiv funktion är: motsatsen till derivatan.
Derivatan av VadDå blir x^3? Det har du redan löst, och fått korrekt svar (x^4 )/4+ C, där C kan vara precis vilken konstant som helst. Derivatan av en konstant är ju noll.
Värdet av den här funktionen för x=1 blir 1^4+C, och om det ska bli 1 så måste C vara lika med noll. Det ser du också ut att ha löst, även om du inte skriver ut tankegången tydligt.
Besvarar detta de frågor du hade?
EDIT Korrigerade, delar nu med 4
När du tar fram en primitiv funktion som du har gjort det så har du tagit fram en primitv funktion som mycket riktigt är då den uppfyller villkoret att när jag deriverar den så blir den . Alltså som ska gälla.
Jag skulle dock hävda (och det är så ;)) att det finns fler förslag på primitiva funktioner till exempelvis dessa
Nästan samma fast med olika konstanter. Dessa uppfyller också samma villkor eftersom när vi deriverar en konstant blir den alltid 0.
Det är därför du lägger till "+C " när du tar fram en primitiv funktion, som jag också ser att du skrivit först
Uppgiften har dock gett dig lite extra information om funktionen nämligen att F(1)=1 som gör att du kan ta reda på konstanten. Uttrycket F(1)=1 betyder att för x-värdet 1 i den primitiva funktionen blir funktionsvärdet(y) lika med 1. Sätter du in dessa villkor i din primitiva funktion så är endast C obekant och går att bestämma. Som föregående talare skrev så kan det vara så att du gjort detta utan att visa det, men det kan också bara vara så att du råkade få fram rätt funktion för att konstanten var lika med noll. Oavsett så hade du behövt redovisa denna uträkning/resonemang.
Hänger du med?
Reglerna för primitiva funktioner är kravet att när du deriverar den primitiva funktionen så skall du få tillbaka den ursprungliga funktionen. Därav kan man alltid genom detta kontrollera om man fått fram rätt primitiv funktion.
Här är hur jag brukar tänka, "derivera baklänges)
ex. bestäm primitiv funktion till
1) När jag deriverar en potensfunktion så brukar jag minska exponenten med 1, det betyder att innan den ska deriveras måste expontenten vara 1 högre, alltså för en primitiv funktion måste jag istället höja expontenten med 1 alltså
2) Är jag klar nu? Om jag testar och derivera och ser om jag får tillbaka det jag ska nämligen då. Hmm om jag deriverar så blir det ju enligt driveringsreglerna . Det liknar ju det jag skulle komma fram till men är 6 gånger för stort. Jag märker då att jag måste "kompensera" genom att dividera med 6, på samma sätt som man måste kompensera genom att multiplicera när man deriverar. Alltså borde en av de primitiva funktionerna till vara .
När man löst sådant ett tag inser man snabbt att reglerna för primitiva funktionerna till potensfunktioner lyder motsatt mot derivata som är
Men ett tips är att det aldrig är fel att försöka tänka baklänges klura och fixa till och kompensera för problem som uppstår. Om du hittat en primitv funktion och det gäller att derivatan av den blir din urpsrungliga funktion så har du hittat rätt alltså .
För egen träning kan det vara intressant att försöka ta fram primitiva funktioner till andra funktioner som du redan känner till derivatorna till.
Om du kan hur man deriverar
Bubo skrev:Antiderivata är inte ett helt korrekt ord, men det är praktiskt och beskriver precis vad en primitiv funktion är: motsatsen till derivatan.
Derivatan av VadDå blir x^3? Det har du redan löst, och fått korrekt svar (x^4 )/4+ C, där C kan vara precis vilken konstant som helst. Derivatan av en konstant är ju noll.
Värdet av den här funktionen för x=1 blir 1^4+C, och om det ska bli 1 så måste C vara lika med noll. Det ser du också ut att ha löst, även om du inte skriver ut tankegången tydligt.
Besvarar detta de frågor du hade?
EDIT Korrigerade, delar nu med 4
Jag får fram F(1) = . Menar du att C är 0? Varför?
Jonto skrev:Reglerna för primitiva funktioner är kravet att när du deriverar den primitiva funktionen så skall du få tillbaka den ursprungliga funktionen. Därav kan man alltid genom detta kontrollera om man fått fram rätt primitiv funktion.
Här är hur jag brukar tänka, "derivera baklänges)
ex. bestäm primitiv funktion till
1) När jag deriverar en potensfunktion så brukar jag minska exponenten med 1, det betyder att innan den ska deriveras måste expontenten vara 1 högre, alltså för en primitiv funktion måste jag istället höja expontenten med 1 alltså
2) Är jag klar nu? Om jag testar och derivera och ser om jag får tillbaka det jag ska nämligen då. Hmm om jag deriverar så blir det ju enligt driveringsreglerna . Det liknar ju det jag skulle komma fram till men är 6 gånger för stort. Jag märker då att jag måste "kompensera" genom att dividera med 6, på samma sätt som man måste kompensera genom att multiplicera när man deriverar. Alltså borde en av de primitiva funktionerna till vara .
När man löst sådant ett tag inser man snabbt att reglerna för primitiva funktionerna till potensfunktioner lyder motsatt mot derivata som är
Men ett tips är att det aldrig är fel att försöka tänka baklänges klura och fixa till och kompensera för problem som uppstår. Om du hittat en primitv funktion och det gäller att derivatan av den blir din urpsrungliga funktion så har du hittat rätt alltså .
För egen träning kan det vara intressant att försöka ta fram primitiva funktioner till andra funktioner som du redan känner till derivatorna till.
Om du kan hur man deriverar
Det stämmer inte att: utan följande gäller:
, följande ekvation gäller för att bestämma :
(Ah, tomast80, vilken miss, det var inte så bra. Tyvärr går inte att redigera nu i efterhand så bra att du Skrev en kommentar om det)
tomast80 skrev:, följande ekvation gäller för att bestämma :
Så man kan säga att rätt svar är:
Där C är 3/4.
Nej, det är inte rätt svar (men du är nära). Läs igenom frågan en gång till, och se till att du svarar på rätt sak.
lillaoski skrev:tomast80 skrev:, följande ekvation gäller för att bestämma :
Så man kan säga att rätt svar är:
Där C är 3/4.
Som tidigare har nämnts så har oändligt många primitiva funktioner. Dessa kan skrivas , där varje möjligt värde på konstanten ger en specifik primitiv funktion.
Din uppgift är att ta reda på vilken av alla dessa primitiva funktioner som uppfyller villkoret .
Du har korrekt bestämt det värde på som gör att villkoret uppfylls, nu saknas bara att beskriva just den primitiva funktionen.
Yngve skrev:lillaoski skrev:tomast80 skrev:, följande ekvation gäller för att bestämma :
Så man kan säga att rätt svar är:
Där C är 3/4.
Som tidigare har nämnts så har oändligt många primitiva funktioner. Dessa kan skrivas , där varje möjligt värde på konstanten ger en specifik primitiv funktion.
Din uppgift är att ta reda på vilken av alla dessa primitiva funktioner som uppfyller villkoret .
Du har korrekt bestämt det värde på som gör att villkoret uppfylls, nu saknas bara att beskriva just den primitiva funktionen.

Jag ser inget x. Det är inte mycket till funktion.
Att är en primitiv funktion till innebär att .
Din primitiva funktion ska alltså vara ett uttryck som beror av och som är sådant att dess derivata är lika med , dvs .
Exempel:
- är en primitiv funktion till eftersom derivatan av är lika med .
- är en primitiv funktion till eftersom derivatan av är lika med .
Ditt förslag till primitiv funktion har inte den egenskapen att dess derivata är lika med .







