Använda Kirchhoff för att beräkna ström och spänning över resistor med superposition

Hej!

Jag sitter med frågan nedan:

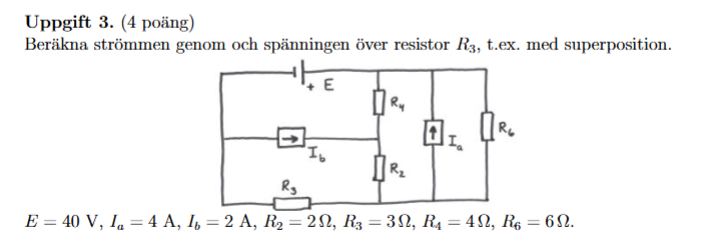
Jag har lite problem här. Bidraget från $I_a$ var enkelt att räkna ut genom att inse att $R_4$ och $R_2$ satt i serie och tillsammans parallelt med $R_6$. Då kunde man ställa upp sambandet $I_3R_3=(I_a-I_3)R_{246}$ enligt Kirchhoff.

Jag försöker använda ett liknande resonmenang för att räkna ut strömbidraget från $I_b$ men det är tydligen krångligare. Jag tänker att kretsen vi då analyserar är:

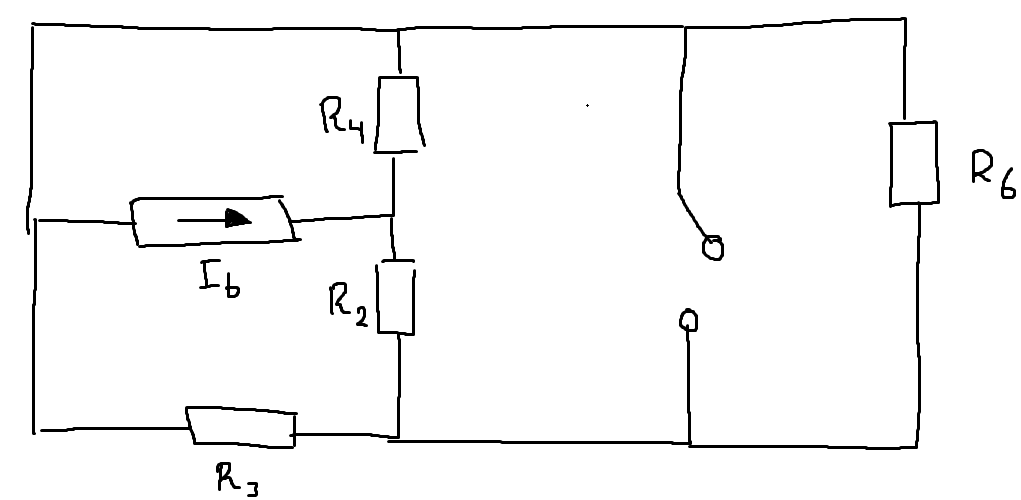
Det jag tänker hittills är att spänninsfallen över $R_2$ och $R_3$ sammanlagt måste vara samma som spänningsfallet över $R_4$ och som spänningsfallet över $R_2$ och $R_6$ sammanlagt. Alltså måste vi ha

$I_2R_2+I_3R_3=I_2R_2+I_6R_6=I_4R_4$

De första två ekvationerna ger tillsammans

$I_3R_3=I_6R_6$

Dessutom vet vi att summan av vissa delströmmar måste ge $I_b$:

$I_3+I_4+I_6=I_b$

Men jag lyckas inte använda dessa ekvationer för att bestämma $I_3$. Kan man använda det jag har tagit fram här?