Beräkna kurvintegral mha Greens sats
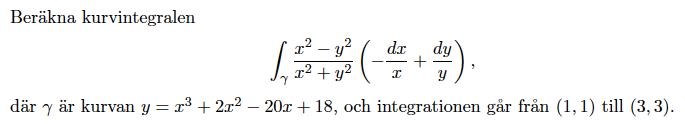
jag gör såhär

Men jag kommer fastna med vilka gränser jag ska ha i mina två integraler. ena kommer ju iallfall vara men den andra, hur ska man göra då? OM man vill lösa denna med Green (vilket man borde kunnagöra eftersom vi inte är i någon singularitet, och det är ett slutet område)
Din ena partiella derivata är fel; är inte lika med noll. Med rätt beräkning ser du att någonting väldigt trevligt händer när du använder Greens formel. (Något som också öppnar upp för att kunna använda många andra metoder!).
MEN, vi måste först undersöka fältets singulariteter, av vilka det finns många. I alla fall där eller är fältet odefinierat p.g.a. nolldivision, och faktum är att -axeln går rätt igenom både kurvan och området där du tänkt använda Greens formel.

Detta gör att Greens formel definitivt inte är tillämpbar, och det går heller inte att lägga till någon annan kurva på något smidigt sätt eftersom själva kurvan vi söker skär -axeln.
Jag misstänker dock att du inte förväntas kunna hantera en sån här lurig situation, och att uppgiften helt enkelt är felkonstruerad (men jag kan ha fel; har du kanske ett facit vi kan titta på?). Kurvintegralen är nämligen divergent.
Här är en annan tråd där vi diskuterade samma problem och kom fram till att det förmodligen är fel i uppgiften:
https://www.pluggakuten.se/trad/kurvintegralen/
Kanske du kan kontakta de som gjort uppgiften och påpeka att något är fel?
AlvinB skrev:Din ena partiella derivata är fel; är inte lika med noll. Med rätt beräkning ser du att någonting väldigt trevligt händer när du använder Greens formel. (Något som också öppnar upp för att kunna använda många andra metoder!).
MEN, vi måste först undersöka fältets singulariteter, av vilka det finns många. I alla fall där eller är fältet odefinierat p.g.a. nolldivision, och faktum är att -axeln går rätt igenom både kurvan och området där du tänkt använda Greens formel.
Detta gör att Greens formel definitivt inte är tillämpbar, och det går heller inte att lägga till någon annan kurva på något smidigt sätt eftersom själva kurvan vi söker skär -axeln.
Jag misstänker dock att du inte förväntas kunna hantera en sån här lurig situation, och att uppgiften helt enkelt är felkonstruerad (men jag kan ha fel; har du kanske ett facit vi kan titta på?). Kurvintegralen är nämligen divergent.
Ooooh. Okej... Men om man vill lösa en sådan typ av uppg, hur hade man gjort då? bara av ren nyfikenhet=)
Vi låtsas att kurvan inte skär -axeln och att integralen då går att beräkna.
Vi ser att
. (Fältet är ett potentialfält!)
Detta öppnar för flera möjligheter:
- Lägga till ett kurvstycke till med en enkel integral så att området sluts och beräkna integralen med Greens formel.
- Ta fram en potentialfunktion och beräkna integralen som en skillnad av värden (som man gör med en envariabelintegral!)
- Utnyttja att integraler längs alla kurvor mellan samma punkter i ett potentialfält är lika så att du kan byta ut kurvan mot vilken kurva som helst som börjar i och slutar i . (Detta blir ungefär samma som metod 1).
Vi kan reparera uppgiften genom att byta kurvan mot . Pröva gärna att räkna ut denna med någon (eller flera!) av metoderna.
Hej,
Om man provar variabelbytet och så blir
och
så
och
så
varför
.
Kurvintegralen kan därför skrivas
där kurvan --- som är kurvan uttryckt i variablerna och --- parametriserats med hjälp av och .
för och
där mängderna och förmodligen är svåra att uttrycka explicit.
Som du ser är integranden väldigt enkel att hantera, medan det är kurvan som är komplicerad; man ser direkt att integranden har primitiv funktion . Om uppgiften hade varit en enkelintegral så hade den varit löst vid detta laget, men nu är uppgiften inom Flervariabelanalys, så då får man inte glömma variabeln också.
AlvinB skrev:Vi låtsas att kurvan inte skär -axeln och att integralen då går att beräkna.
Vi ser att
. (Fältet är ett potentialfält!)
Detta öppnar för flera möjligheter:
- Lägga till ett kurvstycke till med en enkel integral så att området sluts och beräkna integralen med Greens formel.
- Ta fram en potentialfunktion och beräkna integralen som en skillnad av värden (som man gör med en envariabelintegral!)
- Utnyttja att integraler längs alla kurvor mellan samma punkter i ett potentialfält är lika så att du kan byta ut kurvan mot vilken kurva som helst som börjar i och slutar i . (Detta blir ungefär samma som metod 1).
Vi kan reparera uppgiften genom att byta kurvan mot . Pröva gärna att räkna ut denna med någon (eller flera!) av metoderna.
Men tänkte mer om den skärde(skar?) x-axeln, och man ändå vill räkna ut det? Kanske blir komplex analys då istället?
sannakarlsson1337 skrev:AlvinB skrev:Vi låtsas att kurvan inte skär -axeln och att integralen då går att beräkna.
Vi ser att
. (Fältet är ett potentialfält!)
Detta öppnar för flera möjligheter:
- Lägga till ett kurvstycke till med en enkel integral så att området sluts och beräkna integralen med Greens formel.
- Ta fram en potentialfunktion och beräkna integralen som en skillnad av värden (som man gör med en envariabelintegral!)
- Utnyttja att integraler längs alla kurvor mellan samma punkter i ett potentialfält är lika så att du kan byta ut kurvan mot vilken kurva som helst som börjar i och slutar i . (Detta blir ungefär samma som metod 1).
Vi kan reparera uppgiften genom att byta kurvan mot . Pröva gärna att räkna ut denna med någon (eller flera!) av metoderna.
Men tänkte mer om den skärde(skar?) x-axeln, och man ändå vill räkna ut det? Kanske blir komplex analys då istället?
Nja. Det är faktiskt så att integralen då divergerar (= har inget värde). Visa att det är så gör man helt enkelt genom att ställa upp integralen man skulle få om man använde en parametrisering (som i det här fallet blir helt hemsk!) och på något sätt försöker visa att den divergerar.
AlvinB skrev:sannakarlsson1337 skrev:AlvinB skrev:Vi låtsas att kurvan inte skär -axeln och att integralen då går att beräkna.
Vi ser att
. (Fältet är ett potentialfält!)
Detta öppnar för flera möjligheter:
- Lägga till ett kurvstycke till med en enkel integral så att området sluts och beräkna integralen med Greens formel.
- Ta fram en potentialfunktion och beräkna integralen som en skillnad av värden (som man gör med en envariabelintegral!)
- Utnyttja att integraler längs alla kurvor mellan samma punkter i ett potentialfält är lika så att du kan byta ut kurvan mot vilken kurva som helst som börjar i och slutar i . (Detta blir ungefär samma som metod 1).
Vi kan reparera uppgiften genom att byta kurvan mot . Pröva gärna att räkna ut denna med någon (eller flera!) av metoderna.
Men tänkte mer om den skärde(skar?) x-axeln, och man ändå vill räkna ut det? Kanske blir komplex analys då istället?
Nja. Det är faktiskt så att integralen då divergerar (= har inget värde). Visa att det är så gör man helt enkelt genom att ställa upp integralen man skulle få om man använde en parametrisering (som i det här fallet blir helt hemsk!) och på något sätt försöker visa att den divergerar.
ja okej.. hehe då går vi inte in på den ^^ tack så mkt!


