Beräkna trianglar

Du ser ju att den största triangeln har arean $a$ $dm^2$. När du delar upp den till andra så har varje triangel plötsligt $\frac{a}{4}$ $dm^2$ i area. Sedan delar du varje av dessa trianglar i...ja, hur många delar?

woozah skrev:

Du ser ju att den största triangeln har arean $a$ $dm^2$. När du delar upp den till andra så har varje triangel plötsligt $\frac{a}{4}$ $dm^2$ i area. Sedan delar du varje av dessa trianglar i...ja, hur många delar?

Tyvärr hänger jag inte med där. Vart får du a/4 ifrån? 

Tyvärr hänger jag inte med där. Vart får du a/4 ifrån? 

Hur många lika stora trianglar finns det i triangel 2? Hur stor area har var och en av dessa trianglar?

Den första (största) triangeln har arean $a$ $dm^2$. Sedan delas den i fyra lika stora delar. Vardera av dessa har då arean:

$a\cdot \frac{1}{4}=\frac{a}{4}$ $dm^2$.

Smaragdalena skrev:

Tyvärr hänger jag inte med där. Vart får du a/4 ifrån? 

Hur många lika stora trianglar finns det i triangel 2? Hur stor area har var och en av dessa trianglar?

Det finns 4 lika stora trianglar i 2, samt 7 lika stora trianglar i 7. Ska jag då sätta in respekt 4 och 7 i a/4?

Nej, det finns 7 OLIKA stora trianglar i figur 3. Rita in den upp-och-ner-vända triangeln i de tre stora trianglarna i figur 3 och räkna igen!

Smaragdalena skrev:

Nej, det finns 7 OLIKA stora trianglar i figur 3. Rita in den upp-och-ner-vända triangeln i de tre stora trianglarna i figur 3 och räkna igen!

Ursäkta jag skrev fel. Jag menade 7 olika trianglar i 3. Alltså figur 3. O självklart inte 7 olika trianglar i 7. Haha. Men hur gör jag efter det? 

Du vill ha reda på hur många LIKA stora trianglar det finns i varje figur. Som jag skrev i mitt förra inlägg:

Rita in den upp-och-ner-vända triangeln i var och en av de tre stora trianglarna i figur 3 och räkna igen!

Blev det tydligare med den tillagda fetningen?

Smaragdalena skrev:

Du vill ha reda på hur många LIKA stora trianglar det finns i varje figur. Som jag skrev i mitt förra inlägg:

Rita in den upp-och-ner-vända triangeln i var och en av de tre stora trianglarna i figur 3 och räkna igen!

Blev det tydligare med den tillagda fetningen?

Tyvärr hänger jag inte med där. Det är 4 lika stora trianglar och en mindre i figur 3.

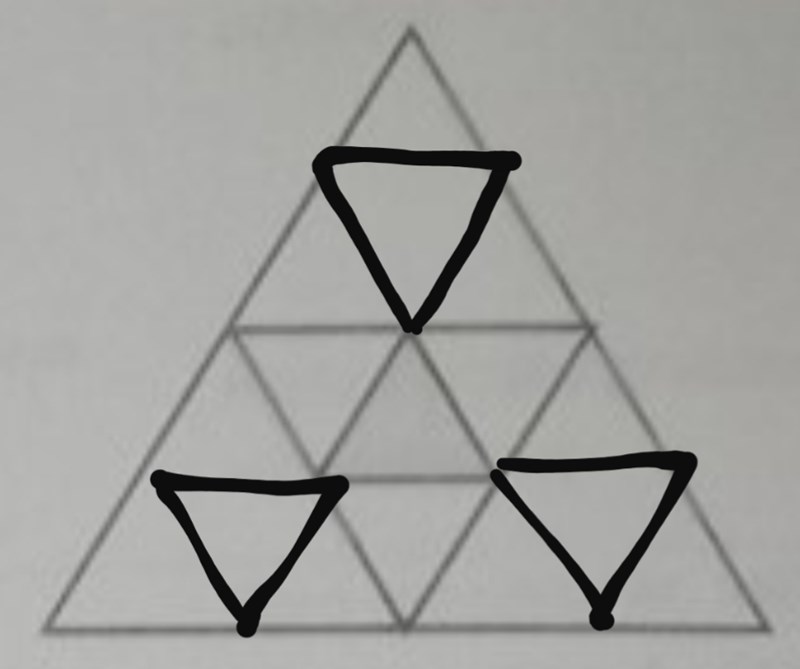
I figur 3 finns det 3 stora och 4 små trianglar (förutom hela triangeln, som naturligtvis består av en enda jättetriangel). Om du ritar in en liten uppochnervänd triangel i var och en av de tre stora trianglar som saknar denna - hur många små trianglar blir det då? Vilken area har var och en av de små trianglarna, om hela den största triangeln har arean $A$?

Smaragdalena skrev:

I figur 3 finns det 3 stora och 4 små trianglar (förutom hela triangeln, som naturligtvis består av en enda jättetriangel). Om du ritar in en liten uppochnervänd triangel i var och en av de tre stora trianglar som saknar denna - hur många små trianglar blir det då? Vilken area har var och en av de små trianglarna, om hela den största triangeln har arean $A$?

Jag får till det till 12 små trianglar. Stämmer det? 

anonymousnina skrev:

Jag får till det till 12 små trianglar. Stämmer det? 

Ja det blir 12 små trianglar till, men hur många småtrianglar blir det då totalt?

Yngve skrev:

anonymousnina skrev:

Jag får till det till 12 små trianglar. Stämmer det? 

Ja det blir 12 små trianglar till, men hur många småtrianglar blir det då totalt?

16 små tillsammans. 

anonymousnina skrev:

16 små tillsammans. 

Ja. Och av dessa 16 trianglar är 1 blå (den i mitten). Hur stor area har då den blå triangeln i tredje bilden?

Yngve skrev:

anonymousnina skrev:

16 små tillsammans. 

Ja. Och av dessa 16 trianglar är 1 blå (den i mitten). Hur stor area har då den blå triangeln i tredje bilden?

Gör jag det genom att sätta in 16 i a/4? dvs - 16/4? 

anonymousnina skrev:

Gör jag det genom att sätta in 16 i a/4? dvs - 16/4? 

Nej. Det stora triangeln i bild 1 har arean $a$ $dm^3$.

I bild 3 är denna triangel delad i 16 lika stora delar.

Varje del har då arean $\frac{a}{16}$ $dm^3$.

Yngve skrev:

anonymousnina skrev:

Gör jag det genom att sätta in 16 i a/4? dvs - 16/4? 

Nej. Det stora triangeln i bild 1 har arean $a$ $dm^3$.

I bild 3 är denna triangel delad i 16 lika stora delar.

Varje del har då arean $\frac{a}{16}$ $dm^3$.

Menar du dm^2 istället för dm^3? Då det står dm^2 i uppgiften.

Det betyder att varje del är 0.0625 dm^2. 

anonymousnina skrev:

Menar du dm^2 istället för dm^3? Då det står dm^2 i uppgiften.

Det betyder att varje del är 0.0625 dm^2. 

Haha, ja jag menar $dm^2$. Bra fångat!

Jag önskar att jag kunde säga att jag skrev så bara för att kolla om du hängde med, men det vore ljug.

Slarvfel av mig helt enkelt.

Arean är helt enkelt $\frac{a}{16}$ $dm^2$, eller om du vill skriva som ett decimaltal, $0.0625a$ $dm^2$.

Du glömde skriva $a$ i ditt svar.

Yngve skrev:

anonymousnina skrev:

Menar du dm^2 istället för dm^3? Då det står dm^2 i uppgiften.

Det betyder att varje del är 0.0625 dm^2. 

Haha, ja jag menar $dm^2$. Bra fångat!

Jag önskar att jag kunde säga att jag skrev så bara för att kolla om du hängde med, men det vore ljug.

Slarvfel av mig helt enkelt.

Arean är helt enkelt $\frac{a}{16}$ $dm^2$, eller om du vill skriva som ett decimaltal, $0.0625a$ $dm^2$.

Du glömde skriva $a$ i ditt svar.

Haha, sånt händer! 
Ok, så nu är uppgift A besvarad. 
Men på B förstår jag inte ens vad de frågar efter? vad är n:te triangeln? 

anonymousnina skrev:

Haha, sånt händer! 

Ok, så nu är uppgift A besvarad. 
Men på B förstår jag inte ens vad de frågar efter? vad är n:te triangeln? 

Triangel 1 är den 1:a (första) triangeln.

Triangel 2 är den 2:a (andra) triangeln.

Triangel 3 är den 3:e (tredje) triangeln.

...

Triangel n är den n:te triangeln.

Yngve skrev:

anonymousnina skrev:

Haha, sånt händer! 

Ok, så nu är uppgift A besvarad. 
Men på B förstår jag inte ens vad de frågar efter? vad är n:te triangeln? 

Triangel 1 är den 1:a (första) triangeln.

Triangel 2 är den 3:a (andra) triangeln.

Triangel 3 är den 3:e (tredje) triangeln.

...

Triangel n är den n:te triangeln.

Aha okej. Alltså verkar typ helt omöjligt för mig att lösa uppgiften. Vilket område i ma3 går igenom det här? ):

Den 3:e bokstaven i alfabetet är C, den 21:e är U och den n:te beror på värdet av n.

Det n:te avser vilken triangel i ordning som arean ska beräknas.

Då n=1 (första triangeln) så är arean a, då n=2 så är arean a/4, då n=3 är den a/16.

Ser du ett mönster mellan n och arean?

Du kan ange arean på de tre första med hjälp av n ... och du kan även ange arean för den n:te, dvs "vilken som helst" baserat på värdet på n.

Euclid skrev:

Den 3:e bokstaven i alfabetet är C, den 21:e är U och den n:te beror på värdet av n.

Det n:te avser vilken triangel i ordning som arean ska beräknas.

Då n=1 (första triangeln) så är arean a, då n=2 så är arean a/4, då n=3 är den a/16.

Ser du ett mönster mellan n och arean?

Du kan ange arean på de tre första med hjälp av n ... och du kan även ange arean för den n:te, dvs "vilken som helst" baserat på värdet på n.

Visa spoiler

$a_n=\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$4^{n-1}$}\right.$

Och hur kan jag då beräkna fram arean på n:te triangeln? 

anonymousnina skrev:

...

Vilket område i ma3 går igenom det här? ):

Jag tror att avsnitten om mönster (typ "Teckna ett uttryck för antalet tändstickor i figur n"  o.s.v.) ingår i åk 9 eller Matte 1.

Aha okej. Alltså verkar typ helt omöjligt för mig att lösa uppgiften. Vilket område i ma3 går igenom det här? ):

Det räcker med Ma1 för den här uppgiften, åtminstone för del a och b.

Den första triangeln har arean $a$.

Den andra triangeln har arean $\frac{1}{4}\cdot a$.

Den tredje triangeln har arean $\frac{1}{4}\cdot \frac{1}{4}\cdot a$.

Den fjärde triangeln skulle ha arean $\frac{1}{4}\cdot \frac{1}{4}\cdot \frac{1}{4}\cdot a$

Vilken area har triangel nummer n?

anonymousnina skrev:

Och hur kan jag då beräkna fram arean på n:te triangeln? 

Ett bra tips om du vill ha mer hjälp är att klicka på de rosafärgade delarna i svaren du får.

Det är dold text som kommer fram om du klickar på den.

Euclid döpte sin dolda text till "Visa spoiler", Smaragdalena döpte sin till "Tips".

Euclid skrev:

Den 3:e bokstaven i alfabetet är C, den 21:e är U och den n:te beror på värdet av n.

Det n:te avser vilken triangel i ordning som arean ska beräknas.

Då n=1 (första triangeln) så är arean a, då n=2 så är arean a/4, då n=3 är den a/16.

Ser du ett mönster mellan n och arean?

Du kan ange arean på de tre första med hjälp av n ... och du kan även ange arean för den n:te, dvs "vilken som helst" baserat på värdet på n.

Visa spoiler

$a_n=\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$4^{n-1}$}\right.$

Alltså a21= 1/4/4^21-1 ? 

anonymousnina skrev:

Alltså a21= 1/4/4^21-1 ? 

Nej det stämmer inte. Du tappar bort $a$-et igen, du har en 4 för mycket och du behöver skriva parenteser runt exponenten så att det blir tydligt vad du menar.

Om vi kallar arean hos figur 1 för $A_1$, figur 2 för $A_2$ och så vidare så får vi att

• $A_1=\frac{a}{4^{1-1}}=\frac{a}{4^0}=a$.
• $A_2=\frac{a}{4^{2-1}}=\frac{a}{4^1}=\frac{a}{4}$. Detta kan även skrivas a/4^(2-1)=a/4^1=a/4.
• $A_3=\frac{a}{4^{3-1}}=\frac{a}{4^2}$. Detta kan även skrivas a/4^(3-1)=a/4^2.
• $A_4=\frac{a}{4^{4-1}}=\frac{a}{4^3}$. Detta kan även skrivas a/4^(4-1)=a/4^3.

...

• $A_{21}=\frac{a}{4^{21-1}}=\frac{a}{4^{20}}$. Detta kan även skrivas a/4^(21-1)=a/4^20.

Yngve skrev:

anonymousnina skrev:

Alltså a21= 1/4/4^21-1 ? 

Nej det stämmer inte. Du tappar bort $a$-et igen, du har en 4 för mycket och du behöver skriva parenteser runt exponenten så att det blir tydligt vad du menar.

Om vi kallar arean hos figur 1 för $A_1$, figur 2 för $A_2$ och så vidare så får vi att

• $A_1=\frac{a}{4^{1-1}}=\frac{a}{4^0}=a$.
• $A_2=\frac{a}{4^{2-1}}=\frac{a}{4^1}=\frac{a}{4}$. Detta kan även skrivas a/4^(2-1)=a/4^1=a/4.
• $A_3=\frac{a}{4^{3-1}}=\frac{a}{4^2}$. Detta kan även skrivas a/4^(3-1)=a/4^2.
• $A_4=\frac{a}{4^{4-1}}=\frac{a}{4^3}$. Detta kan även skrivas a/4^(4-1)=a/4^3.

...

• $A_{21}=\frac{a}{4^{21-1}}=\frac{a}{4^{20}}$. Detta kan även skrivas a/4^(21-1)=a/4^20.

Hur kan jag beräkna den sammanlagda arean samt omkretsen?

anonymousnina skrev:

Hur kan jag beräkna den sammanlagda arean samt omkretsen?

Den sammanlagda arean av de $n$ första trianglarna är $A_1+A_2+A_3+...+A_n$, dvs $a+\frac{1}{4}a+\frac{1}{4^2}a+\frac{1}{4^3}a+...\frac{1}{4^{n-1}}a$ $dm^2$

Det är alltså en summa av termer där kvoten mellan två närliggande termer är konstant.

En sådan summa kallas för geometrisk summa. Känner du till det begreppet?

--------

Vi tar det där med omkretsen sen.

Yngve skrev:

anonymousnina skrev:

Hur kan jag beräkna den sammanlagda arean samt omkretsen?

Den sammanlagda arean av de $n$ första trianglarna är $A_1+A_2+A_3+...+A_n$, dvs $a+\frac{1}{4}a+\frac{1}{4^2}a+\frac{1}{4^3}a+...\frac{1}{4^{n-1}}a$ $dm^2$

Det är alltså en summa av termer där kvoten mellan två närliggande termer är konstant.

En sådan summa kallas för geometrisk summa. Känner du till det begreppet?

--------

Vi tar det där med omkretsen sen.

Ja det gör jag. Då kan jag använda mig av formeln för geometriska talföljdens summa: 

sn=a+ak+ak2+...+akn−1=a(kn−1)/k−1 där k ej får vara 1 för då blir allt noll och då går det inte att använda formeln. 

Vi vet att A1 är a dm^2; men hur kan jag beräkna fram kvoten? 

anonymousnina skrev:

Ja det gör jag. Då kan jag använda mig av formeln för geometriska talföljdens summa: 

 

sn=a+ak+ak2+...+akn−1=a(kn−1)/k−1 där k ej får vara 1 för då blir allt noll och då går det inte att använda formeln. 

Vi vet att A1 är a dm^2; men hur kan jag beräkna fram kvoten? 

Kvoten $k$ får du fram genom att dividera ett tal i talföljden med det närmast föregående talet.

Enklast är att ta $k=\frac{A_2}{A_1}$.

Kontrollera även ditt svar genom att ta t.ex. $\frac{A_3}{A_2}$. Denna kvot ska vara lika med $k$.

Yngve skrev:

anonymousnina skrev:

Ja det gör jag. Då kan jag använda mig av formeln för geometriska talföljdens summa: 

 

sn=a+ak+ak2+...+akn−1=a(kn−1)/k−1 där k ej får vara 1 för då blir allt noll och då går det inte att använda formeln. 

Vi vet att A1 är a dm^2; men hur kan jag beräkna fram kvoten? 

Kvoten $k$ får du fram genom att dividera ett tal i talföljden med det närmast föregående talet.

Enklast är att ta $k=\frac{A_2}{A_1}$.

Kontrollera även ditt svar genom att ta t.ex. $\frac{A_3}{A_2}$. Denna kvot ska vara lika med $k$.

Vet tyvärr inte hur jag ska applicera det på den här uppgiften. 
Om det t.ex. gällde talföljden 5,10,20 osv... så hade jag bara delat 10/5 för att få fram kvoten - vilket då blir 2. Alltså jag förstår hur man använder formeln men inte hur jag kan applicera det på denna uppgift. 
Kan det vara något i stil med att det är 16 små trianglar i figur 3 och 12 små trianglar i figur 2 --> 16/12=1,33? kvoten=1,33? 

anonymousnina skrev:

Vet tyvärr inte hur jag ska applicera det på den här uppgiften. 
Om det t.ex. gällde talföljden 5,10,20 osv... så hade jag bara delat 10/5 för att få fram kvoten - vilket då blir 2. Alltså jag förstår hur man använder formeln men inte hur jag kan applicera det på denna uppgift. 
...

Ja om följden vore 5, 10, 20 o.s.v. så skulle du ta andra talet delat med första talet, dvs 10/5 och  då få fram att kvoten var 2.

Om följden istället vore 1, 1/2, 1/4 o.s.v. så skulle du ta andra talet delat med första talet, dvs (1/2)/1 och då få fram att kvoten var 1/2, eller hur?

Den följd du har i uppgiften är a, a/4, a/16 o.s.v. Kvoten får du på exakt samma sätt som ovan, dvs genom att ta andra talet delat med första talet, ďvs (a/4)/a.

Yngve skrev:

anonymousnina skrev:

Vet tyvärr inte hur jag ska applicera det på den här uppgiften. 
Om det t.ex. gällde talföljden 5,10,20 osv... så hade jag bara delat 10/5 för att få fram kvoten - vilket då blir 2. Alltså jag förstår hur man använder formeln men inte hur jag kan applicera det på denna uppgift. 
...

Ja om följden vore 5, 10, 20 o.s.v. så skulle du ta andra talet delat med första talet, dvs 10/5 och  då få fram att kvoten var 2.

Om följden istället vore 1, 1/2, 1/4 o.s.v. så skulle du ta andra talet delat med första talet, dvs (1/2)/1 och då få fram att kvoten var 1/2, eller hur?

Den följd du har i uppgiften är a, a/4, a/16 o.s.v. Kvoten får du på exakt samma sätt som ovan, dvs genom att ta andra talet delat med första talet, ďvs (a/4)/a.

Ok då får jag kvoten till 0.25.

Men när jag sedan ska använda formeln, ska jag ta kvoten upphöjt till något, vad detta är vet jag inte i detta fall.

Du är på rätt väg.

Den allmänna formeln för en geometrisk summa är

$S_n=\frac{a_1·(k^n-1)}{k-1}$

där Sn är summan av de n första talen i talföljden, a1 är det första talet i talföljden, och k är kvoten mellan ett tal i talföljden och det föregående talet i talföljden (k ≠ 1).

$k=\frac{{\displaystyle \raisebox{1ex}{$a_1$}\!\left/ \!\raisebox{-1ex}{$4^{n-1}$}\right.}}{{\displaystyle \raisebox{1ex}{$a_1$}\!\left/ \!\raisebox{-1ex}{$4^{n-2}$}\right.}}=\frac{4^{n-2}}{4^{n-1}}=4^{n-2}·4^{-(n-1)}=4^{n-2}·4^{1-n}=4^{(n-2)+(1-n)}=4^{-1}=\frac{1}{4}$

Ok då får jag kvoten till 0.25.

Men när jag sedan ska använda formeln, ska jag ta kvoten upphöjt till något, vad detta är vet jag inte i detta fall.

För figur 1 skall du få fram $a\cdot 1$. Vad skalldu ta 0,25 upphöjt till för att det skall bli 1?

För figur 2 skall du få fram $a\cdot\frac{ 1}{4}$. Vad skalldu ta 0,25 upphöjt till för att det skall bli $\frac{1}{4}$?

För figur 3 skall du få fram $a\cdot \frac{1}{16}$. Vad skalldu ta 0,25 upphöjt till för att det skall bli $\frac{1}{16}$?

Ser du något samband mellan figurens nummer och det tal du skall upphöja 0,25 till?

2 w1Smaragdalena skrev:

Ok då får jag kvoten till 0.25.

Men när jag sedan ska använda formeln, ska jag ta kvoten upphöjt till något, vad detta är vet jag inte i detta fall.

För figur 1 skall du få fram $a\cdot 1$. Vad skalldu ta 0,25 upphöjt till för att det skall bli 1?

För figur 2 skall du få fram $a\cdot\frac{ 1}{4}$. Vad skalldu ta 0,25 upphöjt till för att det skall bli $\frac{1}{4}$?

För figur 3 skall du få fram $a\cdot \frac{1}{16}$. Vad skalldu ta 0,25 upphöjt till för att det skall bli $\frac{1}{16}$?

Ser du något samband mellan figurens nummer och det tal du skall upphöja 0,25 till?

För figuf 3: 0.25 upphöjt till 2 för att få 1/16

För figur 2: 0.25 upphöjt till 1 för att få 1/4

För figur 1: 0.25 upphöjt till 0 för att få 1.

Det ökas alltså med 1 varje gång. Det betyder att figur 4 blir då 0.25 upphöjt till 3 =0.015625

Det stämmer. Vad skall du upphöja 0,25 till för att få andelsen av arean i figur nummer $n$?

Smaragdalena skrev:

Det stämmer. Vad skall du upphöja 0,25 till för att få andelsen av arean i figur nummer $n$?

Vad menar du?

anonymousnina skrev:

Smaragdalena skrev:

Det stämmer. Vad skall du upphöja 0,25 till för att få andelsen av arean i figur nummer $n$?

Vad menar du?

För att få fram figur 1 upphöjer man 0,25 till 0. För att få fram figur 2 upphöjer man 0,25 till 1. För att få fram figur 3 upphöjer man 0,25 till 2. För att få fram figur 41 upphöjer man 0,25 till3. För att få fram figur 5 upphöjer man 0,25 till 4. För att få fram figur 6 upphöjer man 0,25 till 5. För att få fram figur 7 upphöjer man 0,25 till 6. För att få fram figur 8 upphöjer man 0,25 till 7. För att få fram figur 9 upphöjer man 0,25 till 8. För att få fram figur 10 upphöjer man 0,25 till 9. För att få fram figur 11 upphöjer man 0,25 till 10. För att få fram figur 12 upphöjer man 0,25 till 11. För att få fram figur 13 upphöjer man 0,25 till 12. Ser du mönstret? Vad skall man upphöja 0,25 till för att få fram figur n?

(Jag hoppade över faktiorn a i alla uträkningar för att det skulle bli tydligare.)

Smaragdalena skrev:

anonymousnina skrev:

Visa föregående citat

Smaragdalena skrev:

Det stämmer. Vad skall du upphöja 0,25 till för att få andelsen av arean i figur nummer $n$?

Vad menar du?

För att få fram figur 1 upphöjer man 0,25 till 0. För att få fram figur 2 upphöjer man 0,25 till 1. För att få fram figur 3 upphöjer man 0,25 till 2. För att få fram figur 41 upphöjer man 0,25 till3. För att få fram figur 5 upphöjer man 0,25 till 4. För att få fram figur 6 upphöjer man 0,25 till 5. För att få fram figur 7 upphöjer man 0,25 till 6. För att få fram figur 8 upphöjer man 0,25 till 7. För att få fram figur 9 upphöjer man 0,25 till 8. För att få fram figur 10 upphöjer man 0,25 till 9. För att få fram figur 11 upphöjer man 0,25 till 10. För att få fram figur 12 upphöjer man 0,25 till 11. För att få fram figur 13 upphöjer man 0,25 till 12. Ser du mönstret? Vad skall man upphöja 0,25 till för att få fram figur n?

(Jag hoppade över faktiorn a i alla uträkningar för att det skulle bli tydligare.)

Hänger med på allt annat men inte figur n

För figur 1 upphöjer du 0,25 till 1-1=0.

För figur 2 upphöjer du 0,25 till 2-1=1.

För figur 3 upphöjer du 0,25 till 3-1=2.

För figur 4 upphöjer du 0,25 till 4-1=3.

För figur 5 upphöjer du 0,25 till 5-1=4.

För figur $n$ upphöjer du 0,25 till...

Smaragdalena skrev:

För figur 1 upphöjer du 0,25 till 1-1=0.

För figur 2 upphöjer du 0,25 till 2-1=1.

För figur 3 upphöjer du 0,25 till 3-1=2.

För figur 4 upphöjer du 0,25 till 4-1=3.

För figur 5 upphöjer du 0,25 till 5-1=4.

För figur $n$ upphöjer du 0,25 till...

Visa spoiler

n-1

Ok så det är alltså svaret på C. När jag räknar omkretsen, ska jag räkna precis som jag räknar med en triangel? 

Nej, du är nästan framme vid svaret på fråga b, om jag inte har missförstått något - men du har inte formulerat svaret än, vad jag kan se. Du skall alltså skriva slutet av meningen:

SVAR: Arean av den n:te triangeln är...

Smaragdalena skrev:

Nej, du är nästan framme vid svaret på fråga b, om jag inte har missförstått något - men du har inte formulerat svaret än, vad jag kan se. Du skall alltså skriva slutet av meningen:

SVAR: Arean av den n:te triangeln är...

Jag tror vi är på uppgift C nu.

E29 E29Euclid skrev:

Smaragdalena skrev:

Nej, du är nästan framme vid svaret på fråga b, om jag inte har missförstått något - men du har inte formulerat svaret än, vad jag kan se. Du skall alltså skriva slutet av meningen:

SVAR: Arean av den n:te triangeln är...

Jag tror vi är på uppgift C nu.

Jaa trodde jag med. 

Smaragdalena skrev:

Nej, du är nästan framme vid svaret på fråga b, om jag inte har missförstått något - men du har inte formulerat svaret än, vad jag kan se. Du skall alltså skriva slutet av meningen:

SVAR: Arean av den n:te triangeln är...

Arean av den n:te triangeln är: a/4^n-1 
Eller ska jag skriva det på den geometriska talföljdens formel? Dvs: A(1-0,25^N)/1-0,25? 

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Smaragdalena skrev:

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Summan. Så då gäller det  A(1-0,25^N)/1-0,25. 

anonymousnina skrev:

Smaragdalena skrev:

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Summan. Så då gäller det  A(1-0,25^N)/1-0,25. 

Du har kastat om några delar i formeln för den geometrisk summan. Scrolla upp lite så ser du hur jag först räknade ut kvoten, sedan applicerade den på formeln och till sist testade resultatet.

Euclid skrev:

anonymousnina skrev:

Visa föregående citat

Smaragdalena skrev:

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Summan. Så då gäller det  A(1-0,25^N)/1-0,25. 

Du har kastat om några delar i formeln för den geometrisk summan. Scrolla upp lite så ser du hur jag först räknade ut kvoten, sedan applicerade den på formeln och till sist testade resultatet.

Står i min matte bok att den allmänna formeln är tvärtom om k är mindre än 1 vilket det är här då der är 0.25!

anonymousnina skrev:

Euclid skrev:

Visa föregående citat

anonymousnina skrev:

Smaragdalena skrev:

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Summan. Så då gäller det  A(1-0,25^N)/1-0,25. 

Du har kastat om några delar i formeln för den geometrisk summan. Scrolla upp lite så ser du hur jag först räknade ut kvoten, sedan applicerade den på formeln och till sist testade resultatet.

Står i min matte bok att den allmänna formeln är tvärtom om k är mindre än 1 vilket det är här då der är 0.25!

Jasså. Det är inte så att du blandar ihop det med nämnaren i en geometrisk serie?

222 E29Euclid skrev:

anonymousnina skrev:

Visa föregående citat

Euclid skrev:

anonymousnina skrev:

Visa föregående citat

Smaragdalena skrev:

Läs uppgiften igen, så att du förstår vad det är du skall räkna ut i c-uppgiften.

Summan. Så då gäller det  A(1-0,25^N)/1-0,25. 

Du har kastat om några delar i formeln för den geometrisk summan. Scrolla upp lite så ser du hur jag först räknade ut kvoten, sedan applicerade den på formeln och till sist testade resultatet.

Står i min matte bok att den allmänna formeln är tvärtom om k är mindre än 1 vilket det är här då der är 0.25!

Jasså. Det är inte så att du blandar ihop det med nämnaren i en geometrisk serie?

Hänger tyvärr inte med längre. 

Hur ser formeln för en geometrisk summa ut? Använd gärna formelskrivaren, så att det går att tuyda det du skriver.

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Euclid skrev:

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

-----

Hur går jag vidare till att lösa omkretserna? 

Förslagsvis:

1) Bestäm omkretsen för triangel 1. Den är liksidig.

2) Använd att:

$areaskalan=(langdskalan)^2\Rightarrow$

$langdskalan=\sqrt{areaskalan}$

anonymousnina skrev:

Euclid skrev:

Visa föregående citat

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

 

Nej, det är a(1-0,25^n)/(1-0,25).

Det du skriver skulle du få fel för.

Laguna skrev:

anonymousnina skrev:

Visa föregående citat

Euclid skrev:

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

 

Nej, det är a(1-0,25^n)/(1-0,25).

Det du skriver skulle du få fel för.

Lite extra ansträngning är aldrig fel:

$S_n=\frac{a·(1-0,{25}^n)}{1-0.25}$

Laguna skrev:

anonymousnina skrev:

Visa föregående citat

 

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

 

Nej, det är a(1-0,25^n)/(1-0,25).

Det du skriver skulle du få fel för.

Det du har skrivit är $a\frac{(1-0,25^n)}{1}-0,25$, och det var inte det du menade, eller hur?

(ändrade N till n också - stora och små bokstäver är inte samma sak i matematik)

Euclid skrev:

Laguna skrev:

Visa föregående citat

anonymousnina skrev:

Euclid skrev:

Visa föregående citat

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

 

Nej, det är a(1-0,25^n)/(1-0,25).

Det du skriver skulle du få fel för.

Lite extra ansträngning är aldrig fel:

$S_n=\frac{a·(1-0,{25}^n)}{1-0.25}$

Självklart. Jag skriver från mobilen men det var det jag menade. 

Deanonymousnina skrev:

Euclid skrev:

Visa föregående citat

Laguna skrev:

anonymousnina skrev:

Visa föregående citat

Euclid skrev:

Laguna skrev:

Nina och Euklid har väl samma formel (förutom glömda parenteser och A i stället för a)? 

Du har rätt. Jag stirrade mig blind på nämnaren ...

@Nina: C-uppgiften är klar.  

Så svaret på C är alltså:

A(1-0,25^N)/1-0,25?

 

Nej, det är a(1-0,25^n)/(1-0,25).

Det du skriver skulle du få fel för.

Lite extra ansträngning är aldrig fel:

$S_n=\frac{a·(1-0,{25}^n)}{1-0.25}$

Självklart. Jag skriver från mobilen men det var det jag menade. 

Hur gör jag med uppgift D gällande omkretsen? 

Det har du redan fått tips om:

tomast80 skrev:

Förslagsvis:

1) Bestäm omkretsen för triangel 1. Den är liksidig.

2) Använd att:

$areaskalan=(langdskalan)^2\Rightarrow$

$langdskalan=\sqrt{areaskalan}$

E29 deSmaragdalena skrev:

Det har du redan fått tips om:

tomast80 skrev:

Förslagsvis:

1) Bestäm omkretsen för triangel 1. Den är liksidig.

2) Använd att:

$areaskalan=(langdskalan)^2\Rightarrow$

$langdskalan=\sqrt{areaskalan}$

Får ändå inte till den sista. Arean är ju dm upphöjt till två, är det lika med längdskalan upphöjt till två alltså? 

Det stämmer. Arean ändras en faktor $\frac{1}{4}$ mellan varje triangel. Det innebär att förändringen av längdskalan (och därmed också omkretsen) kan beräknas enligt:

$langdskalan=\sqrt{\frac{1}{4}}=...$