Bestämma de tangenter till y=f(x) som går genom P=(0,-11)
 Hej!
Hej!
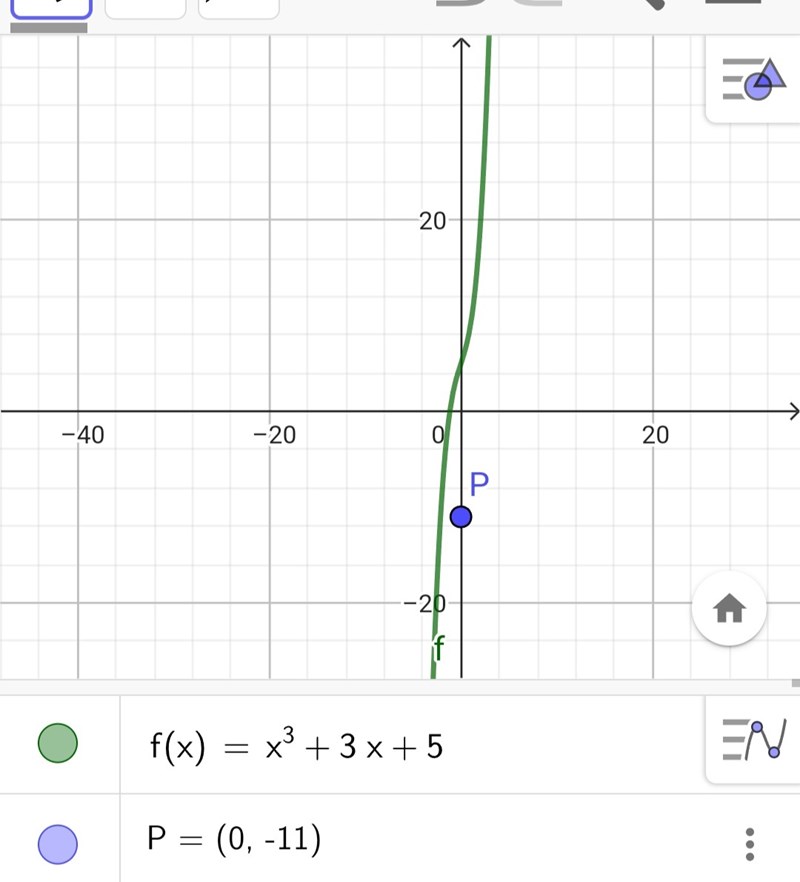
"Bestäm de tangenter till y=f(x) (om det finns några) som går genom punkten P=(0,-11), där f(x)=x^3+3x+5. "
jag ritade funktionen i geogebra och hittade denna tangent nedan. Har jag tänkt och gjort rätt? Jag kan ej tänka mig det finns fler tangenter pga hur kurvan ser ut.
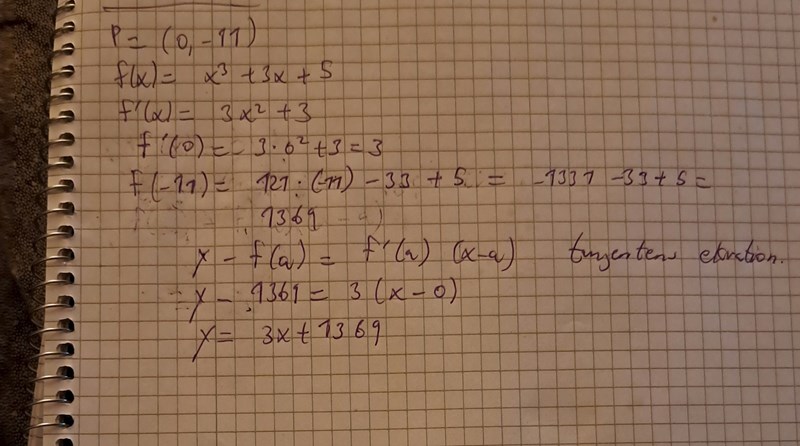
Hej.
Nja, du beräknar f'(0), men det värdet har inget med den efterfrågade tangenten att göra.
Jag hjälpte alldeles nyss till i en tråd med en väldigt likartad fråga. Läs den frågan och svar #24.
Yngve skrev:Hej.
Nja, du beräknar f'(0), men det värdet har inget med den efterfrågade tangenten att göra.
Jag hjälpte alldeles nyss till i en tråd med en väldigt likartad fråga. Läs den frågan och svar #24.
Det var ganska rörig tråd så jag tänkte skapa min egen här. Ok varför har mitt värde inget med den efterfrågade tangenten att göra? Vi söker ju tangenter som går genom punkten P.
Går funktionen genom punkten (0,-11)? Om den gör det kan det vara intressant att ta reda på f'(x), inte annars.
destiny99 skrev:
Det var ganska rörig tråd så jag tänkte skapa min egen här.
Läs bara själva frågan och svar #24
Ok varför har mitt värde inget med den efterfrågade tangenten att göra? Vi söker ju tangenter som går genom punkten P.
f'(0) anger funktionens lutning vid x = 0.
Den behöver inte vara lika stor som funktionens lutning I tangeringspunkten.
Yngve skrev:destiny99 skrev:Det var ganska rörig tråd så jag tänkte skapa min egen här.
Läs bara själva frågan och svar #24
Super! Det hjälpte mig nu.
Smaragdalena skrev:Går funktionen genom punkten (0,-11)? Om den gör det kan det vara intressant att ta reda på f'(x), inte annars.
Nej det står inget om att funktionen går genom punkten.
destiny99 skrev:
Ok varför har mitt värde inget med den efterfrågade tangenten att göra? Vi söker ju tangenter som går genom punkten P.
f'(0) är grafens lutning vid x = 0, dvs lutningen på den linje som tangerar grafen vid x = 0. Jag har ritat in den linjen lite grovt i bilden.
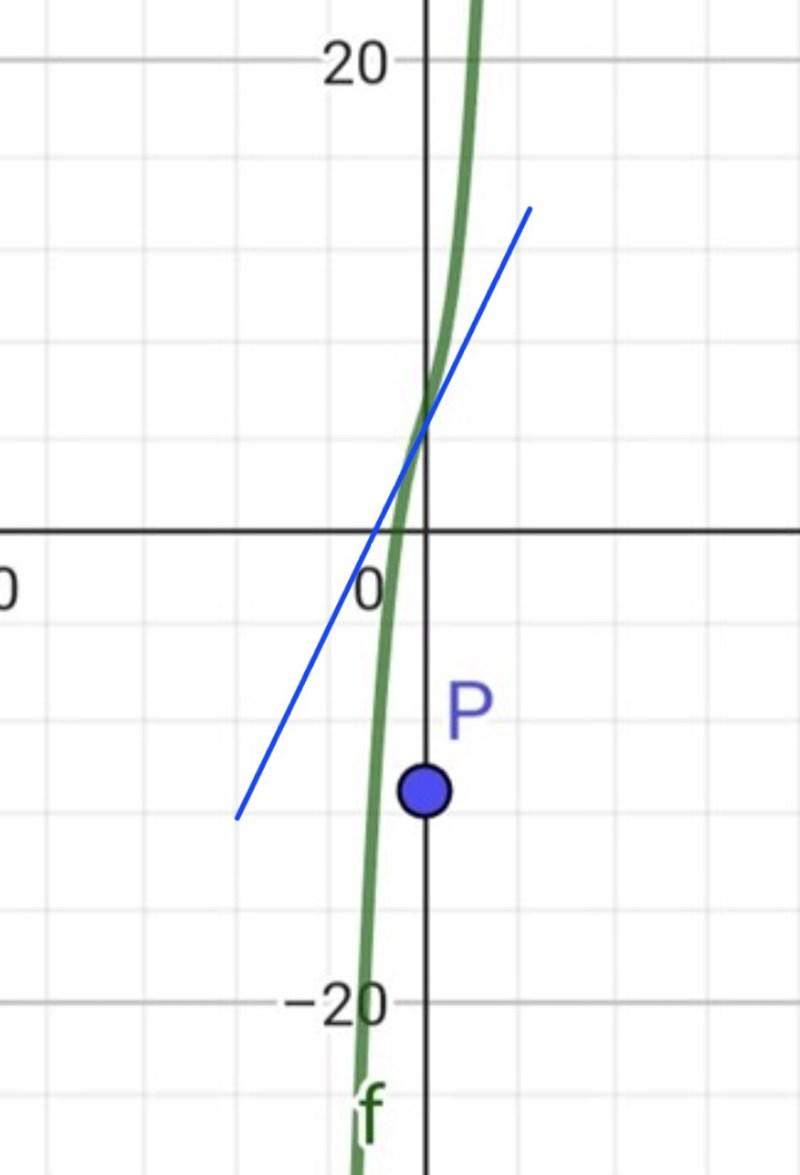
Drt är inte den tangenten som avses, eftersom den inte går genom den givna punkten.
Yngve skrev:destiny99 skrev:Ok varför har mitt värde inget med den efterfrågade tangenten att göra? Vi söker ju tangenter som går genom punkten P.
f'(0) är grafens lutning vid x = 0, dvs lutningen på den linje som tangerar grafen vud x = 0. Jag har ritat in den linjen lite grovt i bilden.
Drt är inte den tangenten som avses, eftersom den inte går genom den givna punkten.
Aa ok jag är med nu.
Jag vet ej hur jag löser detta vidare. Har jag gjort detta korrekt?

Det ska nog vara f(a)-y, inte y-f(a).
Laguna skrev:Det ska nog vara f(a)-y, inte y-f(a).
Källa: https://youtu.be/2dbIOtonmoA?si=dc7U8DoXYApSReeH
Funkar ej denna ?
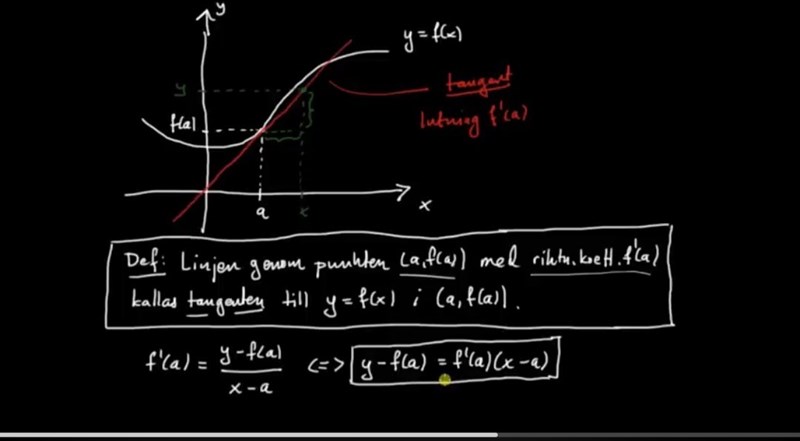
OK, men då ska det inte vara a-x1.
Laguna skrev:OK, men då ska det inte vara a-x1.
Aa juste det ska ju vara (x1-a)




