Hjälpvinkelmetoden
Jag behöver hjälp med uppgift b och c
vad gör jag för fel på b
och vad är a och b i uppgift c


A och b är siffrorna som står framför sin och cos. När det inte står något så kan du själv lägga till *1,för det ändrar ju inte värdet.
Micimacko skrev:A och b är siffrorna som står framför sin och cos. När det inte står något så kan du själv lägga till *1,för det ändrar ju inte värdet.
 hur räknar jag ut v?
hur räknar jag ut v?
Du har själv skrivit tan b/a
Micimacko skrev:Du har själv skrivit tan b/a
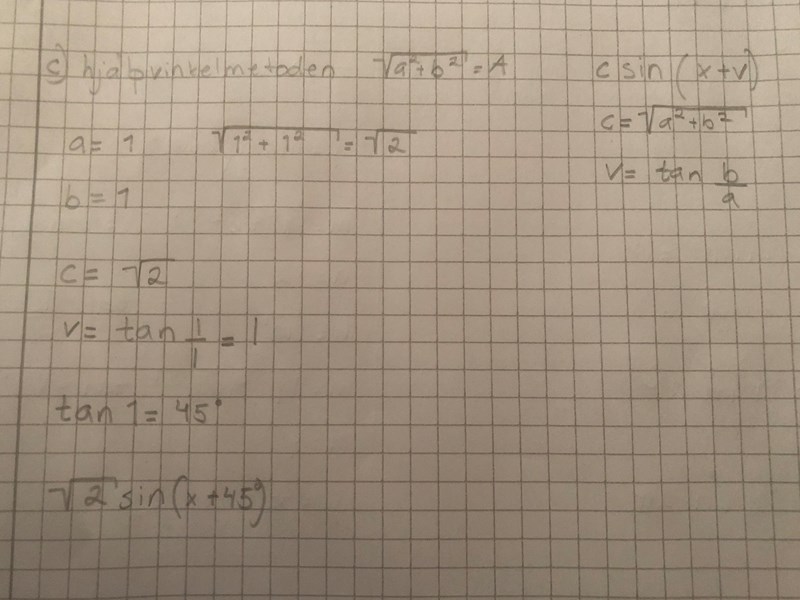 så?
så?
hur löser jag detta nu då?
Micimacko skrev:A och b är siffrorna som står framför sin och cos. När det inte står något så kan du själv lägga till *1,för det ändrar ju inte värdet.
Vad gör jag för fel på uppgift b?
Nu byter du ut sinx + cosx mot det nya uttrycket du har räknat fram. Felet på b ser inte jag heller.
På b): Du har omvandlat 2sinxcosx till 2sinx istället för sin(2x).
Micimacko skrev:Nu byter du ut sinx + cosx mot det nya uttrycket du har räknat fram. Felet på b ser inte jag heller.
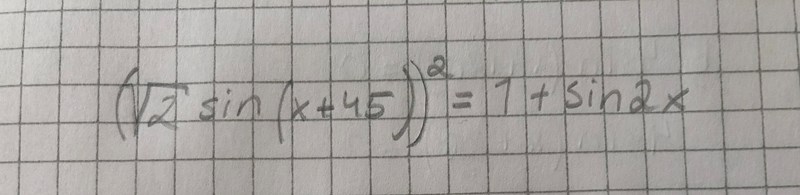 så?
så?
Skaft skrev:På b): Du har omvandlat 2sinxcosx till 2sinx istället för sin(2x).
Tack!
hur kommer jag vidare nu då?
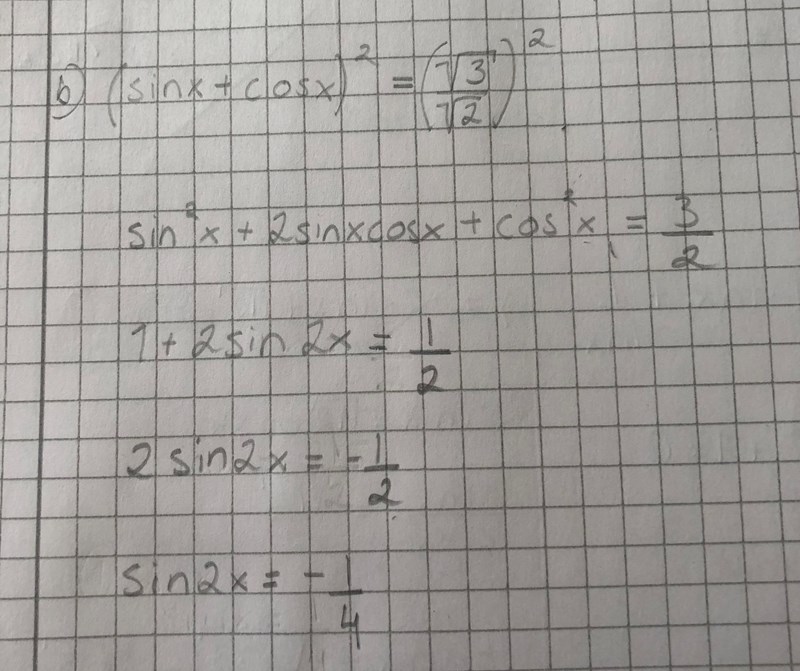
Invers sin på båda sidor, och tänk på dels att det blir två fall, dels perioden.
EDIT: Oj, jag är visst inte tillräckligt uppmärksam.
Vad händer i det här steget?
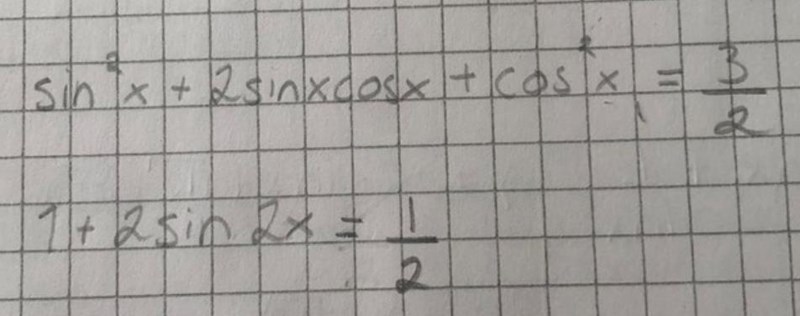
2sinxcosx är inte lika med 2sin(2x), utan med sin(2x). Och hur blev 3/2 bytt till 1/2?
Du tänker säkert rätt men du skriver fel. Det gäller inte att utan istället .
Fråga gärna om detta känns oklart.
Se även detta svar i din andra tråd.

Skaft skrev:Vad händer i det här steget?
2sinxcosx är inte lika med 2sin(2x), utan med sin(2x). Och hur blev 3/2 bytt till 1/2?
det måste ha blivit något konstigt med 1/2 för jag menar givetvis 3/2
Tack!
Yngve skrev:Du tänker säkert rätt men du skriver fel. Det gäller inte att utan istället .
Fråga gärna om detta känns oklart.
Se även detta svar i din andra tråd.
precis, jag tänker så som du skriver och det är jag som skriver fel. Tack!
Skaft skrev:På b): Du har omvandlat 2sinxcosx till 2sinx istället för sin(2x).

hur Löser jag uppgiften?
jag fastnar även på Beatas lösning
 och på uppgift c, jag har inte kommit fram till några lösningar alls
och på uppgift c, jag har inte kommit fram till några lösningar alls
Du gör fortfarande fel i omskrivningen av 2sin(x)cos(x) trots mina två tidigare inlägg. Varför vill du inte sätta det till sin(2x)?
Hej Amanda!
Eftersom jag också håller på med trigonometrin blev jag nyfiken på den här uppgiften.
Jag tog mig friheten att kopiera och komplettera i dina papper. Du hade ju kommit rätt långt på a) och b)
c) var däremot knepig. På b) kunde jag få fram fyra lösningar inom 0 - 360o , men Beatas lösning fick jag bara fram två på och förmodligen Beata också. Där skulle det vara bra om någon annan som jobbat mer med den metoden, berättar hur man ska tänka.

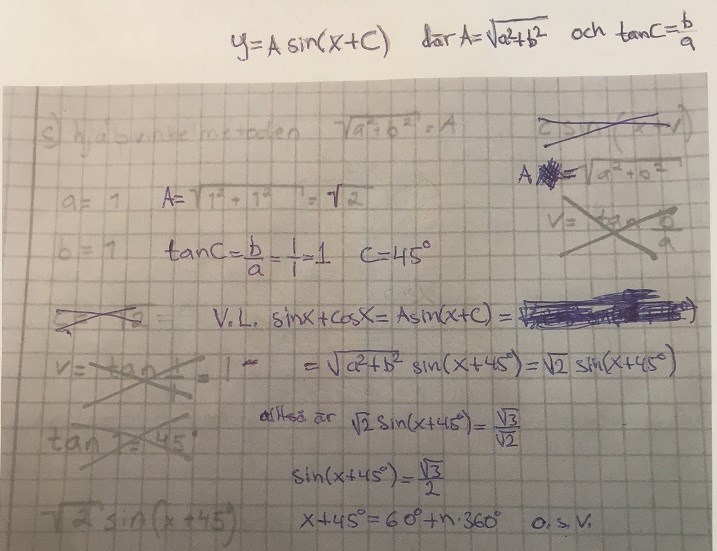
Hoppas att det här hjälper dig en bit på vägen i alla fall.
OK jag ser mitt fel. Jag borde ha kollat med räknaren eller enhetscirkeln. Det finns bara två möjliga värden på x inom intervallet så Beata var nog den som hade rätt!






