Logaritmisk derivering
Hej! Jag förstår verkligen inte hur jag ska tänka i följande. Har använt produktregeln på olika sätt, logaritmerat först och sedan deriverat, för att sen använda produktregeln igen, på olika sätt och ändå får jag aldrig rätt svar. Hoppas någon kan förklara stegvis hur man löser denna. Problemet hos mig ligger nog i de två första stegen där man logaritmerar och deriverar 3^x

Med logaritmisk derivering får du ju:
Om du förenklar det som står till höger med hjälp av logaritmlagarna är det inte särskilt svårt att bestämma derivatan.
Jo.. har börjat så men jag tror att jag gör fel ändå. Har gjort olika försök som sagt, detta är det senaste: 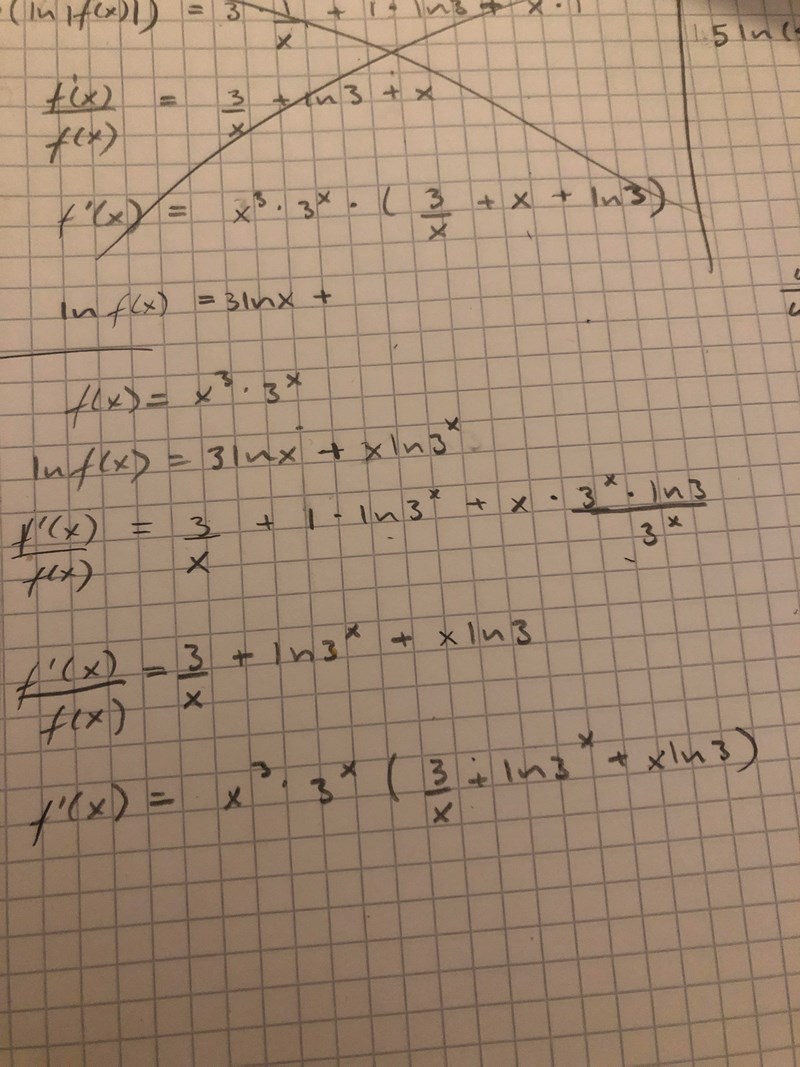
edit: jag ser minst ett fel när jag logaritmerat 3^x nu men gör fel när jag gör rätt där också haha
kan ju skrivas om till . När vi deriverar får vi då:
Vad blir då ?


