Max/min värden - envariabelsanalys

Funktionen blir odefinierad där du (t.ex.) delar med noll (vilket du gör med tan), tar kvadratroten ur ett negativt tal (om vi pratar om reella tal), tar logaritmen av ett negativt tal osv...

Jag har inte listat alla fall, du behöver vara vaksam.

Orsaken till att funktionen ovan är odefinierad för $\frac{\pi}{2}$ är att

$\displaystyle \tan(x)=\frac{\sin(x)}{\cos(x)}$

Och försöker man sätta in $x=\frac{\pi}{2}$ i nämnaren $\cos(x)$ inser man att det blir nolldivision.

Att man gör en viss affär av begreppet "slutet och begränsat intervall" för den kontinuerliga funktionen beror på att det finns en sats som garanterar existensen av ett största- och minsta värde på intervallet givet just dessa egenskaper.

En annan viktig sats för kontinuerliga funktioner på slutna- och begränsade intervall säger att om funktionen antar två värden så måste den anta alla värden däremellan.

Här handlar det (som tur är) inte att bestämma Max/min utan bara avgöra om det finns. Av sarsen som Daniel hänvisar till (”kontinuerliga bilden av en kompakt mängd är kompakt”) följer att det räcker med att visa  kontinuitet på det aktuella slutna och begränsade (=kompakta) intervallet. Detta är  lätt, eftersom nämnaren >=1 och kont där och täljaren är välbekant kontinuerlig.

En start kan väl vara att räkna ut f(0) och f(1).

Här kan vi använda enhetscirkeln.

1) Rita en ring.
2) Rita in x-axeln och y-axeln. Gör y-axeln extra lång uppåt.
3) Markera var 0,5 är på y-axeln.
4) Markera ungefär två sådana längder på cirkeln från x-axeln.

En figur jag ritat för hand kommer här.

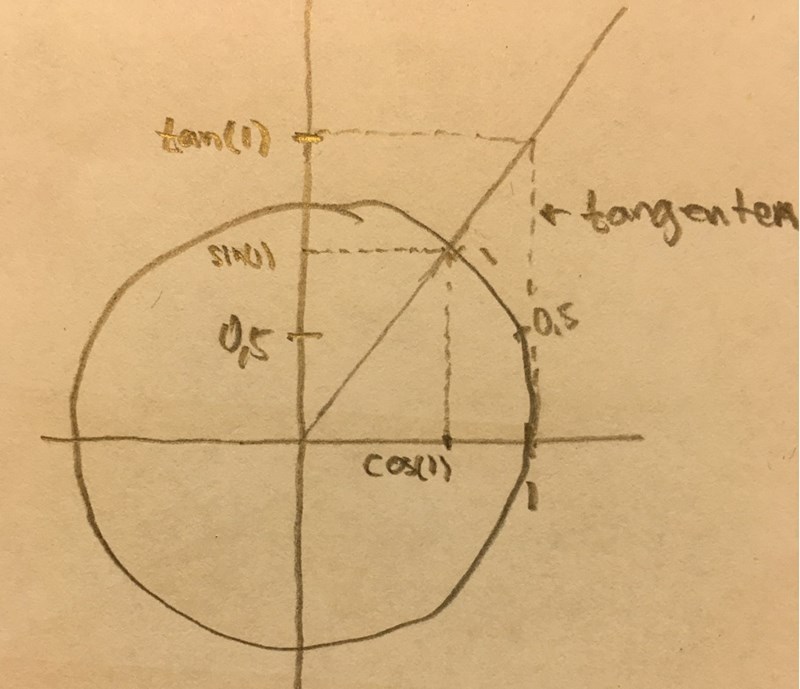
Med hjälp av den så ser du att vi kan konstatera att värdena för sin, och tan kommer att vara kontinuerliga i intervallet .
Med lite grovuppskattning så ser vi att $\sin \left(1\right)\approx 0,8;$ $\tan \left(1\right)\approx 1,4.$(Verkliga värden c:a 0,84 och 1,56)
Använder vi de värdena så ser vi att täljarens värde blir negativt och nämnarens värde positivt.
Då vet vi att vid x=0 har vi ett maxvärde och vid x=1 ett minvärde i intervallet.

OBS att vi använder radianer för vinkeln.
Med hjälp av ett rutat papper kan du komma ännu närmare värdena och använder du passare så blir det bättre ändå.