Diskussionstråd: Ämnesförslag till gymnasiearbeten
För den som vill diskutera eller spåna gemensamt i anslutning till megatråden med gymnasiearbeten, finns denna tråd. Vi kommer att försöka gå igenom denna tråd regelbundet och plocka ut bra idéer och förslag.
Om ni inte vill diskutera publikt, kan ni skicka ett PM till någon av oss moderatorer, så lägger vi in ämnena i huvudtråden. :)
Jag har två kommentarer om de två första matteförslagen.
Den första tycker jag borde placeras i biologi (kalla eventuellt biologi för "biologi/fysiologi") och den är ytlig. Att människan upplever storlekar logaritmiskt är redan etablerat, och infon kan man hitta på wiki. Frågan är bättre ställd som "varför" eller kanske som praktisk undersökning där man vill påvisa detta.
Den andra borde placeras på teknik och programmering.
Jag tycker att alla projekt som involverar att odla krasse eller diverse växter i en modifierad jord för att besvara "hur påverkar X växtlighet", där X är pH, cigarettfimp, salt, wifi-signal, kaliumjodid, schampoo eller whatever, är ovidkommande. Jag har sett för många sådana här på PA men inte vågat skriva det till folk som redan satt igång med sina projekt. Sådana experiment tror jag inte kan ge pålitliga resultat, det är varken intressant för eleven eller för andra eventuella läsar. Systemet är för komplext, variablerna är dåligt definierade och kontrollerade. Ett exempel är kritiken jag gav här för att personen inte hade satt igång än: https://www.pluggakuten.se/trad/gymnasiearbete-svampodling/
Här är några renare förslag jag har på mattefrågor. De första är satser. Det är enkelt att hitta en lärobok och skriva av beviset, men du ska inte göra det utan ge en introduktion till ämnet for kontext, sedan presentera beviset på sådant sätt att det är lättläsligt för en klasskamrat. Språket måste inte vara formellt, men du ska göra dig förstådd. Den andra delen är mer öppen för egen fantasi, det är enkla frågor men med svåra svar, beroende på hur mycket djup man vill gå till. Gemensamt för alla dessa är att din effort och tid kommer gå till förarbetet att förstå dig på ämnet först, det kommer inte synas via att din uppsats blir X sidor lång (den kommer antagligen bli kortare än andras inom andra ämnen), utan att den har kvalité och handlar om ett avancerat ämne. En del av din effort kommer också att gå till att lära dig skriva i , vilket är mycket obligatoriskt.
För vissa av dessa förslag kan det behövas en extern handledare. Kontakta studierektor eller studievägledare vid ett universitet nära dig om de har möjlighet att erbjuda handledning. Du kan självklart också skaffa sig en handledare innan ämnet är bestämt!
Bredvid varje förslag står ungefär vid vilken årskurs man stöter på begreppet/ämnet i en matte/ingenjörsutbildning.
- Hilberts Nullstellensatz (4). Ge en introduktion till ringteori och algebraisk geometri och bevisa och förklara Hilberts Nullstellensatz.
- Abel–Ruffinis sats (3/4). Sätt in dig i gruppteori och förklara varför det inte finns en sluten lösningsformel för en generell femtegradsekvation. Vilka specialfall finns det och hur kommer det sig att dessa funkar?
- Isomorfisatserna (3). Sätt in dig i abstrakt algebra, förklara och bevisa sedan isomorfisatserna för grupper, om du inte hinner så tag endast den första isomorfisatsen.
- Perron–Frobenius sats (2/3). Sätt in dig i linjär algebra och härled Perron-Frobenius sats, förklara speciellt varför det är intuitivt att satsen ska vara sann.
- Analysens huvudsats (1). Sätt in dig i epsilon delta bevis och förklara rigoröst hur det kommer sig att .
- Annan sats. Öppna en lärobok av lämplig svårighetsgrad och välj en sats du gillar eller tror kan vara intressant för andra. Gör sedan som ovan!
- -----------------------------------------
- Tensorer (2). Sätt in dig i linjär algebra. Vad är en tensor och i vilka fysiksammanhang dyker den upp?
- Fourieranalys (2). Ge en introduktion till fourieranalys. Börja med att förklara taylorserier och förklara sedan likheter och skillnader med fourierserier. Förklara intuitionen bakom fourierserieformlens utseende. Vilken är bäst? Vad betyder "bäst"?
- (Komplex) analys (2/3). Exakt vilka krav behöver vi ställa på två funktioner för att de ska vara lika överallt givet att de är lika i en punkt?
- Variationskalkyl (2/3). Förklara varför och bevisa att cirkeln omsluter den största möjliga arean.
- Geometri (2-4). Läs min tråd, utveckla.
- Millenieproblemen. Välj ett av millenieproblemen. Ge kontext till ämnet och förklara millenieproblemet, vad för påverkan skulle en eventuell lösning ha på andra problem? Vilka approaches finns i nuläget, vilka framsteg har gjorts? Varför är frågan svår att lösa? Finns svagare versioner som är bevisade?
- Leta upp en forskningsartikel (). För särskilt begåvade med väldigt bra förkunskaper: hitta en forskningsartikel i ett ämne som intresserar dig. Sortera efter ämne och underkategori på arXiv. Kontakta en relevant forskare och fråga om han/hon skulle kunna tänka sig att handleda dig. Ge en introduktion till ämnet, presentera sedan artikelns resultat nybörjartillgängligt i den mån som är möjligt. Utöka artikelns innehåll med förbättringar eller nya perspektiv.
Vad tycker ni om mina förslag? Jag skulle gärna vilja att de syntes på huvudsidan om de är bra nog.
Extremt bra förslag. Jag är så oerhört imponerad.
Ähumm... är detta verkligen förslag till gymnasiearbeten?
Om jag trott att jag inte var speciellt smart förut så blev jag definitivt övertygad om att jag måste tillhöra någon överlevande mycket tidig primat.
ConnyN skrev:Ähumm... är detta verkligen förslag till gymnasiearbeten?
Om jag trott att jag inte var speciellt smart förut så blev jag definitivt övertygad om att jag måste tillhöra någon överlevande mycket tidig primat.
Jag håller med dig Conny. Att de känns avancerade för att vara gymnasiearbeten, alltså.
Ja, jag är medveten om det, men faktiskt valde jag satserna så att de är intuitiva (efter en bit inläsning), och utmaningen är att eleven sedan ska kunna förmedla något han/hon tycker är självklart för sina läsare på ett formellt men förståeligt sätt. Perron forbenius är till exempel väldigt hands-on och kan konkretiseras med en person som väljer glassmak baserat på vilken glass han åt senast osv... Den om variationskalkyl och cirklar ser nog självklar ut även utan nån inläsning, men där beviset är något att bita i.
Pga (ren) mattes teoretiska natur så tycker jag man har extra tid att lägga ner jämfört med andra som har praktiska delar där det går åt ganska mycket onödig tid till förberedelse/städning/resor/inköp, och då kan man utnyttja det till att grotta ner sig i något riktigt djupt istället. Sen tror jag att man inte väljer gyarb i matte om man inte gillar det väldigt mycket to begin with, faktiskt.
ConnyN skrev:Ähumm... är detta verkligen förslag till gymnasiearbeten?
Om jag trott att jag inte var speciellt smart förut så blev jag definitivt övertygad om att jag måste tillhöra någon överlevande mycket tidig primat.
Så mycket mer involverat än att bygga en Go-cart vilket många på teknik/natur gör är det väl inte? Du ska ändå spendera ganska många månader med att konsolidera och sammanställa information. Som Qetsiyah beskrev är det dessutom inte fråga om att du ska göra någon avancerad framläggning utan du ska främst skriva det som ett expanderat PM i uppsats-format och försöka göra det begripligt för en hypotetisk klasskamrat.
Kom också ihåg att detta alltså handlar om studenter med ett genuint intresse för teoretisk matematik. När jag läste gjorde en klasskamrat ett gymnasiearbete om kvantelektrodynamik som blev väldigt involverat. Denna elev läste universitetsmatematik redan i gymnasiet och tävlade i både matematik samt fysik.
Ja jag har tänkt ett tag nu. Tänk om jag gjorde det oftare innan jag talade så bra världen runt mig skulle bli😊
Om man läser Qetsiyahs förslag en gång till och det han och Ebola har skrivit, så håller jag med om att förslagen är bra.
Möjligen kan man väl önska sig att vi även kunde få ihop lite förslag för den som vill fördjupa sina gymnasiekunskaper.
Statistik, geometri, trigonometri, derivata, integraler, komplexa tal, talteori, funktioner, bevis, m.m. Det finns så mycket under var och en av dessa delar som det skulle vara möjligt att göra ett gymnasiearbete av inbillar jag mig, men sedan beror det givetvis på vad läraren går med på. Där finns det väl många som har större kunskap om detta än mig här på pluggakuten. En lärare jag pratat med ansåg att mitt eget försök till gymnasiearbete angående talet e knappast hade godkänts som förslag i dagens skolor. Idag finns krav om att det ska utföras praktiska försök och mycket datainslag om det ska antas. Är det så?
ConnyN skrev:En lärare jag pratat med ansåg att mitt eget försök till gymnasiearbete angående talet e knappast hade godkänts som förslag i dagens skolor. Idag finns krav om att det ska utföras praktiska försök och mycket datainslag om det ska antas. Är det så?
Intressant fråga. På skolverket finns exempel på gymnasiearbeten på högskoleförberedande program:
Varje av dessa innehåller ett praktiskt/experimentellt moment med tydlig verklighetsanknytning. Det står dock inte uttryckligen någonstans som jag kan se att det är ett krav. Jag känner också till minst två som nyligen gjort helt teoretiska arbeten.
Tre ord: Minimal viable product. Ett gymnasiearbete bör ha ett enkelt och väldefinierat delmål som om det uppfylls resulterar i en godtagbar produkt. Arbeten där man kanske förr eller senare hittar något intressant och bara läser om något är ofta farliga och inte nödvändigtvis intressanta.
Mitt förslag: Undersök gummibands fysik. Finns massor man kan göra med gummiband men låt oss hålla det konkret.
Pitch: Undersök "gummibandspistolen" när man sätter ett gummiband med ena öglan runt tummen, drar bak med andra handen och skjuter iväg den.
Minsta viable kan vara att undersöka hur arbetet man utför när man drar tillbaka gummibandet jämförs med rörelseenergin och hur snabbt gummisnodden rör sig när man skjuter iväg den. Man mäter två energier lite systematiskt. Jämför dem.
I värsta fall har man en Fs-graf och en hastighetsmätning och kan kalla arbetet: En systematisk undersökning av gummipistolens verkningsgrad. Klart i november.
När man väl gjort det kan man fördjupa sig och bygga vidare på artikeln om gummibands fysik om man är intresserad. Exempelvis kan man jämföra lastningskurvan och avlastningskurvan och hur detta relaterar till energiförluster.
Man kan låta gummibandet åldras och se hur styrkan förändras när det torkar ut.
Man kan undersöka hur ett gummiband förlorar spänst genom att överlasta det. Dra ut det förbi gränsen och undersök effekten. Man kan göra en mikroskopistudie av sprickor som uppstår i gummibandet över tid.
Man kan diskutera gummits energiförluster och dess relation till samhällsfrågor så som vad som är ett bra gummidäck.
Gummiband har underliga termiska egenskaper. Se hur styvhet påverkas av temperatur. Om du värmer upp gummibandet blir pistolen bättre eller sämre? Osv.
Man bör börja med något enkelt som fungerar och bygga på det.
Som fysiker så har jag en förkärlek till att helt enkelt göra korellationsstudier med mycket data och lära sig databehandling
Man ska inte underskatta hur lite praktisk erfarenhet naturelever får med undersökande (till skillnad mot informationssökande) i skolan och att ta tillfället till att kanske för första gången någonsin göra en större systematisk undersökning, även om det är något som den med träning tror är enkelt, är bra.
Fallrörelsen hos koner exempelvis är inte i närheten så enkelt eller utforskat som man skulle tro
Pitch: Ta papperscirklar rullade till koner, släpp och låt dem falla från vila. Inledande konstanten kan vara att man har identiska papperscirklar som rullas till olika spetsiga koner. Släpp dem från olika höjder och jämför falltider. Diagrammet med spetsighet (vinkel) på ena axeln och falltid från 2m är grundprodukten.
Visst inte så svårt, gör man ibland i grundskolan men gör massor av koner, go nuts, gör 20 och ha en teoretisk diskussion av luftmotstånd.
Sedan kommer man under processen kunna uppmärksamma aspekter av rörelsen man tycker är intressant och vill bygga på.Är exempelvis vad är luftmotståndet proportionaliteter. Standard är att säga att det är prop mot v eller v^2 men vilket är det. Att mäta hastigheter är svårt. Man kan komma på kluriga upplägg för det.
Det är svårt att kvantifiera men fenomentet där en fallande kon wobblar eller slår runt har jag alltid tyckt är lustigt. En spetsig kon är självstabiliserande men en platt cirkel fladdrar bara runt kaotiskt i fallet. Men skulle aldrig börja där.
Inte min favoritidé men vill ta det som ett exempel på att man kan ta klassiska koncept som alla känner och antingen göra den mer ordentlig eller mer systematiskt än många gjort tidigare
Den första tycker jag borde placeras i biologi (kalla eventuellt biologi för "biologi/fysiologi") och den är ytlig. Att människan upplever storlekar logaritmiskt är redan etablerat, och infon kan man hitta på wiki. Frågan är bättre ställd som "varför" eller kanske som praktisk undersökning där man vill påvisa detta.
Varför är nog en bättre fråga, det är sant.
Den andra borde placeras på teknik och programmering.
Det vet jag inte om jag håller med om. Det borde kanske stå som både och, däremot. RSA-kryptering är en matematisk metod, och det kan finnas fler metoder.
Jag tycker att alla projekt som involverar att odla krasse eller diverse växter i en modifierad jord för att besvara "hur påverkar X växtlighet", där X är pH, cigarettfimp, salt, wifi-signal, kaliumjodid, schampoo eller whatever, är ovidkommande. Jag har sett för många sådana här på PA men inte vågat skriva det till folk som redan satt igång med sina projekt. Sådana experiment tror jag inte kan ge pålitliga resultat, det är varken intressant för eleven eller för andra eventuella läsar. Systemet är för komplext, variablerna är dåligt definierade och kontrollerade. Ett exempel är kritiken jag gav här för att personen inte hade satt igång än: https://www.pluggakuten.se/trad/gymnasiearbete-svampodling/
Detta håller jag inte med om. Det kan absolut vara så att experimentet är för litet eller för specifikt, men det är mer för en student att ta upp och diskutera med sin ansvariga lärare. Det går absolut att undersöka hur exempelvis krasse påverkas av modifierad jord. Det stämmer att det finns många felkällor (även om vissa kan uteslutas genom att exempelvis använda en hydroponisk odling), men det behöver inte betyda att laborationen är meningslös. Det är inte heller ett enormt arbete som efterfrågas i ett gymnasiearbete. Såvitt jag fick lära mig när jag gick i gymnasiet ska vara ett vetenskapligt arbete, för att eleven ska visa att hen kan genomföra ett vetenskapligt arbete, med allt vad det innebär.
Brasklapp angående "vetenskapligt arbete":
När jag gjorde mitt gymnasiearbete (som blev uselt, dock) var det väldigt strikt med den vetenskapliga biten – en frågeställning som sakta raffinerades, en tydligt definierad metod, sammanfattade resultat och därefter en diskussion av dessa resultat. Dock har jag även hört från andra personer, som gått andra gymnasieprogram i andra skolor, att de gjorde helt andra saker, korresponderande till typ "jag byggde en lådbil" istället för "jag undersökte vilken lådbilsmotor som är mest effektiv".
När jag kikar på Skolverkets hemsida verkar det vanligaste vara att göra ett projekt enligt en vetenskaplig arbetsmodell ("vilken lådbilsmotor"), men det finns också förslag som är mer åt "bygga lådbil"-hållet, där själva byggandet är i fokus. Kort sagt: jag vet inte, med andra ord. Om det är projektet som är i fokus, då kanske inte "vad händer om vi ger krasse wifi-uppkoppling?" ett bra ämne att välja, men om det handlar om ett vetenskapligt arbete kan det absolut vara ett bra ämne (okej, kanske inte wifi, med det var ett väldigt roligt förslag :) )
Och innehållet i ovanstående spoiler för mig vidare till dina förslag. Även om de är intressanta, är jag lite tveksam. Dels delar jag Connys (åtminstone inledande) tanke om att dessa förslag känns väldigt svåra, intuitiva eller inte, men framförallt gällande just frågan om ett vetenskapligt arbete. Det går säkert att göra vetenskapliga arbeten inom dessa satser, men att sätta sig in i och förklara en matematisk sats eller ett bevis, så att det kan förklaras för en klasskamrat, är inte ett vetenskapligt arbete. Dina frågor kring Abel-Ruffinis sats, Fourierserier (vilken formel som är "bäst"), komplex analys, variationskalkyler samt millennieproblemen skulle säkert fungera som egna arbeten (om de uppfyller kraven, men det är upp till respektive elevs handledare att avgöra), men de andra skulle nog behöva omformuleras om de ska fungera som vetenskapliga arbeten. Men om de endast ska fungera som projekt, där förklarandet är arbetet, fungerar de säkert.
@SeriousCephalopod: Det låter som en bra poäng att köra lite agil gymnasieprojektsutveckling.
Möjligen kan man väl önska sig att vi även kunde få ihop lite förslag för den som vill fördjupa sina gymnasiekunskaper.
Statistik, geometri, trigonometri, derivata, integraler, komplexa tal, talteori, funktioner, bevis, m.m.
Det vore trevligt också! :)
En hydroponisk odling skulle vara en bra förbättring, men enligt mig kan och borde en gymnasieelev göra bättre än så. Att ett experiment är dåligt kontrollerat och definierat gör ju den ovetenskaplig (och ja, meningslös), menar du att det inte skulle göra det? Jag förstår inte. Jag förklarade min kritik lite mer utförligt i den tråden jag länkade plus hur jag tror den skulle kunna förbättras (genom att göra den vit). Det finns en kurs i bioteknik som heter exakt odlingsteknologi så jag tror att jag vet vad jag pratar om.
Min andra kritik mot sånna gymnasiearbeten är helt enkelt att de är mycket ooriginella. Det bryter självklart inte mot någon av Skolverkets regler, men någonstans känner jag att man själv får ta ansvar att skapa ett projekt, sätta igång sin kreativitet och satsa tid på den så att man efteråt kan vara näjd och stolt med slutprodukten. Jag tycker inte det är i enlighet med sann forskningsanda att betrakta sitt arbete som något man behöver få överstökat, eller som du säger "inte ett enormt arbete". Det är symboliskt viktigt som sista grejen man gör i gymnasiet som utan vilken man inte får sin examen (man brukar inte få underkänt, men signalen Skolverket vill sända är tydlig, det är något viktigt).
Angående mina matteförslag tycker jag man ska ha i åtanke att det är ett väldigt annorlunda ämne jämfört med fysik, kemi och biologi. Därför kommer tillvägagångsättet oundvikligen bli annorlunda. Med en gnutta öppenhet och välvilja från sin handledare i skolan (som med fördel kan vara en mattelärare) skulle man kunna formulera mina förslag sådan att det blir en acceptabel och intressant frågeställning. Skolverkets "krav" på gymnasiearbeten i natur är väldigt vinklade mot just fy/ke/bio, så man blir tvungen att göra egen tolkning (med sin mentor).
När jag gjorde mitt gymnasiearbete fick jag göra en del avstamp från det vanliga tillvägagångssättet. Mitt gymnasiearbete hade ingen verklighetsanknytning eller tillämpning, och jag kommenterade inte detta i uppsatsen. Min rapport följde inte normal labbrapportstruktur, den hade en introduktion, sedan följde mina resultat. Ingen metod, inga felkällor, inga källor, ingen källkritik (som jag ser nu explicit står i skolverkets krav, oops?), ingen bakgrund, ingen diskussion... Den hade ingen praktisk del, men var heller inte en litteraturstudie...
Så länge mentorn förstår att man är seriös så kommer inte formalian (i den utsträckning den existerar) sätta stopp för det. Om man skaffar sig en extern handledare borde det vara trygghetsingivande, vilket några av mina förslag med fördel skulle behöva (ja, jag menar det som det är skrivet). Det är en träning att samarbeta med och få råd av en person man inte tidigare mött och min förhoppning är också att en eventuell extern handledare kan inspirera eleven ytterligare om ämnet och berätta hur det är att forska/plugga/jobba beroende varifrån man får handledaren.
Jag kommer göra en egen tråd om matteförslagen och fler om ke/bio/fy om jag kommer på några, de behöver inte läggas in i megatråden.
Visa spoiler
Jag tillsammans med min handledare från SU fick verkligen slåss för att mitt projekt skulle bli av. I mitt gymnasum var upplägget att man fick lärarna man hade i sin specialiseringskurs (som också gick på våren) som handledare för gymnasiearbetet, för mig blev det en biologi och en kemilärare, superbra... Jag frågade min mattelärare och när hon sa nej så frågade jag två andra, ingen napp. Mina handledare var skeptiska och inte uppmuntrande, ganska trångsynta och otrevliga genom hela processen. Förtvivlad slängde jag iväg ett mail till nån på SU och förväntade mig inte ett svar, men som slutade i att jag fick en en handledare!
Därifrån tog det fart och det var bland de roligaste sakerna jag gjort, och tänk att det varade i en hel termin. Jag vill gärna att andra matteintresserade också får chans att göra gyarb i matte.
Mina handledare från skolan fick inget tack i acknowlegement (tror jag).
En hydroponisk odling skulle vara en bra förbättring, men enligt mig kan och borde en gymnasieelev göra bättre än så. Att ett experiment är dåligt kontrollerat och definierat gör ju den ovetenskaplig (och ja, meningslös), menar du att det inte skulle göra det?
Du är väldigt svartvit i din bedömning här, det är mer det jag ifrågasätter. Nej, det är inte världens bästa projekt, men det är ett projekt, och det kan visst ha vetenskaplig relevans. Det viktigaste är inte att utesluta alla felkällor, utan att ha koll på vilka felkällor som finns. Du har själv kommit med förbättringar – om en får ett vetenskapligt hållbart resultat hänger i detta fall på utförandet, inte idén.
Min andra kritik mot sånna gymnasiearbeten är helt enkelt att de är mycket ooriginella. Det bryter självklart inte mot någon av Skolverkets regler, men någonstans känner jag att man själv får ta ansvar att skapa ett projekt, sätta igång sin kreativitet och satsa tid på den så att man efteråt kan vara näjd och stolt med slutprodukten. Jag tycker inte det är i enlighet med sann forskningsanda att betrakta sitt arbete som något man behöver få överstökat, eller som du säger "inte ett enormt arbete". Det är symboliskt viktigt som sista grejen man gör i gymnasiet som utan vilken man inte får sin examen (man brukar inte få underkänt, men signalen Skolverket vill sända är tydlig, det är något viktigt).
Du läser in saker som jag inte sagt. Jag säger att gymnasiearbetet inte är ett jättestort arbete – och därmed inte kräver världens bästa experiment – inte att det är oviktigt eller tråkigt. Med det sagt tycker jag inte att ens gymnasiearbete måste vara en underbar upplevelse. Om det är det, vad bra! Om inte, så innebär det inte att arbetet garanterat blir dåligt, eller att ämnesområdet inte är något för en som person.
Jag kommer göra en egen tråd om matteförslagen och fler om ke/bio/fy om jag kommer på några, de behöver inte läggas in i megatråden.
Okej! Som sagt, jag är inte emot att lägga in dem i megatråden, och jag är inte emot idén om ett gymnasiearbete i ren matematik heller. Med det sagt vill jag se till att förslagen som läggs in har stor chans att fungera som gymnasiearbeten, och genom att formulera förslagen som frågor som kan besvaras, tror jag att det finns större chanser att ens handledare från skolan accepterar ämnesförslaget. Hur respektive elev sedan väljer att lägga upp sitt arbete, det är deras ensak. :)
Du säger med olika formuleringssätt att gymnasiearbeten inte behöver vara satsiga för att kontra min åsikt som du tycker ligger för långt andra hållet spektrat, har jag förståt rätt? Min avsikt (angående varken krassen eller matten) är inte att hetsa folk till att vara ambitiösta eller göra projektet överdrivet komplicerat för sakens skull eller för att jämföra sig med andra och visa upp sig, det tycker jag är meningslöst. Jag tror med full uppriktighet att gymnasiearbetet blir roligare för en själv om man ser den som en chans och inte ännu en tråkig skoluppgift. Det är alltså en hel termin med avsatt lektionstid och chans att få individuell vägledning och sponsring med material att undersöka nåt man tycker är intressant och som inte betygssätts, för mig låter det som en chans, eller bättre på engelska opportunity. Man får ju ingen igen liknande chans förrän kanske kandidatarbete, men det är inte heller lika fritt.
Man kanske vill prioritera något annat, tex fixa bra betyg i de sista kurserna där betyget faktiskt spelar roll, eller plugga HP sista terminen, det är också ok, men man kan i alla fall ha det jag skrev i baktanken.
Intressanta åsikter och tankar har kommit fram här tycker jag. Tillsammans borde vi kunna få fram bra saker. Vi har sett Qetsiyahs lite mer avancerade förslag för de som gillar utmaningar och kanske ligger i framkant med sina ämeskunskaper. Han visar också att det med lite oortodoxa metoder kan gå att få göra på sitt "eget" sätt. Det är ett bra exempel på att inte låta någon enskild handledare stoppa en elev som verkligen vill något.
Smutstvätt har också bra inlägg i sin spoiler "en frågeställning som sakta raffinerades, en tydligt definierad metod, sammanfattade resultat och därefter en diskussion av dessa resultat". Vilket låter som en mycket bra grundstomme till ett mer vetenskapligt arbetssätt.
SeriousCephalopods lite mer "lets do it" är också bra att tänka på. Det måste inte vara komplicerade uppdrag för att kunna bli intressanta.
En början till ett förslag för ett enklare gymnasiearbete som inkluderar geometri och trigonometri, skulle kunna vara att testa hur noggrant kan man göra en geometrisk uppmätning av ett geografiskt område med så enkla medel som man hade på 1800-talet, då de första riktigt detaljerade kartorna började dyka upp? T.ex. rita upp en tomt eller annat område och sedan jämföra det med en karta från idag och se hur nära man kan komma med kanske lite olika metoder? Man kommer då också in på frågan hur stor noggrannhet är det på en karta från idag och hur stor är noggrannheten för en så pass liten yta i t.ex. Google Maps? Det går säkert att utveckla mer. Det går också för den astronomiskt intresserade att göra en hel del mätningar av planetrörelser och avståndsmätning med hjälp av trigonometri.
Qetsiyah skrev:Du säger med olika formuleringssätt att gymnasiearbeten inte behöver vara satsiga för att kontra min åsikt som du tycker ligger för långt andra hållet spektrat, har jag förståt rätt?
Jag säger att jag tror på att erbjuda ett annat perspektiv också. Våra perspektiv kompletterar varandra lite grann – för vissa kommer gymnasiearbetet att vara superkul, för andra kommer det vara mjeh, och för några kommer det att vara en plåga.
Med det sagt, flera av dina förslag skulle säkert kunna fungera som förslag redan nu. Jag tänker på:
- Varför finns det ingen sluten lösningsformel för en generell femtegradsekvation. Vilka specialfall finns det och hur kommer det sig att dessa funkar?
- Vad är en tensor och i vilka fysiksammanhang dyker den upp?
- Ge en introduktion till fourieranalys. Börja med att förklara taylorserier och förklara sedan likheter och skillnader med fourierserier. Förklara intuitionen bakom fourierserieformlens utseende. Vilken är bäst? Vad betyder "bäst"?
- Exakt vilka krav behöver vi ställa på två funktioner för att de ska vara lika överallt givet att de är lika i en punkt?
- Välj ett av millenieproblemen. Ge kontext till ämnet och förklara millenieproblemet, vad för påverkan skulle en eventuell lösning ha på andra problem? Vilka approaches finns i nuläget, vilka framsteg har gjorts? Varför är frågan svår att lösa? Finns svagare versioner som är bevisade?
Men eftersom du sagt att du vill göra en egen tråd måste jag fråga: Vill du att vi lägger in dessa förslag i megatråden, eller vill du ha dem till din egen tråd? :)
Fortsätter lista förslag.
Bakgrund: Runt årsskiftet 2018-2019 var en tråd om en fråga från en elev som läste Kemi 1 som handlade om avsvalningstid. Vad som påverkar hur snabbt en varm vätska svalnar av i kontakt med luften. Kort därefter gjorde jag en kort mätning hemma (resultat) där jag kollade hur snabbt varmt vatten i en burk svalnade av. Experimentet har några i efterhand uppenbara brister så som avsaknad av aktiv mätning av rumstemperatur, men att ett experiment har brister är poängen.
Pitch 3: Undersök hur varmt vatten avsvalnar. Det konkreta kan vara en jämförelse av avsvalningshastigheten i fyra olika tekoppar. Påverkar en tekopps form hur snabbt mitt te svalnar? (såklart ja, men är effekten värd att bry sig om?). Häll upp lika volymer vatten i fyra olika tekoppar och mät hur temperaturen sjunker över tid. Minimiprodukten är att jämföra graferna och diskutera lite om teorin hos avsvalning.
Den som är teknologi-intresserade kan lära sig sensorteknik och Arduino. Är man mindre teknologisk kan man låna skolans temperatursensorer i labsalen eller göra ett analogs experiment med termometer. Aktiv avläsning kommer göra en galen men frustreras man av det kan man göra kreativa hack-lösningar så som att filmatermometern och sammanfatta från videon i efterhand.
Avsvalning är en sån där sak som universitetsstudenter tror att alla känner till eftersom de läst om Newtons avsvalningslag och kanske gjort några teoriproblem i värmelära men är ärligt talat något som jag diskuterar aktivt (okej, nämner...) i fysik 1 och där fenomentet att temperaturminskningen är som snabbast när det är som varmast är i något ett barn/ungdom absolut inte är aktivt är medveten om. Bara sådana saker kan upptäckas av den individuella eleven.
Sedan upptäcker man som jag gjorde i mitt lilla experiment att avsvalningen avviker från exponentiell avsvalning men jag har inte gått vidare och förklarat effekten. Var det för att glaset värmdes upp inledningsvis? Är avdunsning också viktigt? Påverkades rummets temperatur av vattnet? Vad hände egentligen?
Såklart ska dock poängteras att mina typer av projekt kräver att man har en nyfikenhet kring det lilla och vardagliga och nyanserna i vår vardag - och att metoder för hur man bygger en förståelse från erfarenhet är meningsfulla.
Jag vill göra en egen tråd, jag tror det är bäst för nu blev min lista lite lång och opassande i megatråden (jag har lagt till fler i förrådet). Jag vill skriva fler allmäna råd också som inte strikt är projektförslag, plus nåt förbehåll/kommentar enligt synpunkterna som lyfts här. Men det är ett superbra initiativ i alla fall!
SeriousCephalopod, jag gillar dina förslag men hur ska de organiseras? Vill du skriva kortare (1-2 meningar) beskrivningar och låta listan länka nån annanstans, eller nån annan lösning? Dina förslag är ju aningen för utförliga haha
Okej, då vet jag! :)
Som handledare skulle jag behöva läsa på mer i litteraturen för att se om det verkligen finns en fråga här men jag vart nyfiken ikväll på hur arkimedes princip gäller i gränsen mellan vätska och solid så detta är mer något jag själv skulle vilja undersöka men inte har undersökt.
Idéskiss: Man kan ta en blandning av stärkelse och vatten, variera koncentrationen och se huruvida det är vikten hos det undanträngda vattnet eller bulkmassan eller vad som påverkar lyftkraften. Tillslut börjar ju andra effekter än vätsketryck att dominera och vi får en solid eller seg suspension som kan 'flyta' ting som är tyngre än 'vätskan' och kan vara intressant (för mig) att se en graf med lyftkaft/volymenhet på ena axeln och torrmassa-andel på andra och se en grad som först ökar dugligt linjärt och sedan växer (geometriskt/exponentiellt) när modellen bryter ihop.
Intressant förslag! Får jag lägga in det i tråden? Jag tänker mig typ "Hur fungerar Arkimedes princip när vätskan blir mer trögflytande?" och en länk till din tråd om frågan. :)
Jag skulle vilja lägga ett gott ord om numeriska metoder och mer specifikt Monte Carlo-metoder, eftersom jag inte har sett så mycket sådant här. Området kan självklart variera beroende på vad handledaren och eleven tycker, men jag tänker ge ett förslag för prissättning av optioner. Möjligen att detta är förslag till ett aningen ambitiöst gymnasiearbete, men man behöver inte nödvändigtvis gå djupgående överallt.
Det som behövs är lite bakgrund i grundläggande sannolikhetsteori. Stokastisk variabel, sannolikhetsfördelning (normalfördelningen, som eleven förhoppningsvis känner igen sen statistiken), väntevärde och stora talens lag är nog dom viktigaste koncepten. Stokastisk process (i en enklare mening) för att introducera geometrisk brownsk rörelse som en rimlig modell för någon underliggande värdepapper/aktie. Något argument för riskneutral värdering. Introducera vad en option eller finansiellt derivat är, grundfallet köp-/säljoption. Idén bakom Monte Carlo-metoder.
Nu finns det väldigt mycket olika saker man kan välja att undersöka beroende på intresse, och idén är alltså att använda Monte Carlo för prissättning.
- Undersök priset av en köp-/säljoption under olika modeller för underliggande. Då kan det vara passande att läsa på om Euler-Maruyama metoden.
- Undersök priset av olika optioner och kanske lite mer specifikt exotiska optioner. Jämför priset av olika optioner och fundera varför vissa kanske är dyrare/billigare.
- Undersök hur priset av en köp-/säljoption förändras beroende på exempelvis volatiliteten, startvärde, löptid, eller något annat. Förklara.
- Studera Monte Carlo-metoder i sig och undersök olika variansreduktionstekniker och hur dom fungerar.
- Undersök varför Monte Carlo-metoder fungerar. Då blir det lite mer teoretiskt och gymnasiearbetet handlar mer om sannolikhet, men om man vill kan man även ha något exempel där man använder Monte Carlo.
- Undersök i vilka fall Monte Carlo-metoder är lämpliga som numerisk metod. Vad är bra med den? Vad är dåligt med den?
- (Väldigt ambitiöst) Kolla upp hur man kan beräkna "The Greeks", dvs. känslighetsparametrar som säger oss hur värdet av en option ändras med avseende på exempelvis löptid, volatilitet eller något annat. Antingen teoretiskt (kommutativitet av väntevärde och derivata) eller faktiskt implementera och beräkna några utvalda "Greeks" för någon köp-/säljoption.
- Kombinationer av ovanstående.
I ett sådant här gymnasiearbete så får man in lite grundläggande "programmering" och får testa på numeriska lösningar till annars väldigt svåra problem. Det måste inte vara ett jättefokus på matematiken utan man kan skippa en del detaljer om man vill och fokusera mer på att faktiskt använda metoden och sen jämföra och analysera priser av olika optioner.
Gymnasiearbetet är nog som mest lämpligt för den som är aningen ambitiös och intresserad av programmering, matematik (och finans). Det är ett väldigt "hands-on" exempel på hur matematik faktiskt används i vardagen.
EDIT: Jag förutsätter att alla optioner är av europeisk typ.
De här förslagen gillar jag! Men jag undrar om inte samma personer ovan också kommer säga att dessa förslag är för svåra?
- Den enda statistiken man lär sig i ma1-ma5 är en pytteliten bit i matte1 och sannolikhetslära i ma5.
- För Brownsk rörelse behövs väl en lagom dos äkta analys i form av måtteori? Och åtminstone lite flervariabelanalys?
I vilken utsträckning går det att hoppa över formella detaljer för att komma till det saftiga man kan leka runt med? Jag är inte insatt i det här ämnet så du får förklara.
Det känns som att i alla fall den där grundläggande statistiken behöver förklaras ordentligt (s.v., väntev, stora talens lag som du skrev, men också varians, multivariabla s.v.? ). Hur mycket numeriska metoder tänker du dig att man behöver?
Ja, lite svåra ser de ut att vara, men det kanske kan gå ändå? I kursen matematikspecialisering läser nog vissa lite statistik. Jag föreslår följande förslag:
(Matematik/programmering) Aktiehandeln är idag till stor del automatiserad, med datorprogram som förutser hur priset på olika aktier kommer att utvecklas. Hur fungerar ett sådant program, och varför? Du kan exempelvis välja en specifik metod/algoritm och undersöka hur väl den förutser marknaden, eller jämföra flera olika algoritmers/metoders prestationer. Fler förslag finns här [länk till Moffens inlägg].
Får jag lägga in det i tråden? :)
Projektet blir inte nödvändigtvis enklare om den är vinklad mot programmering (=mer tillämpad), så jag tycker det borde lämnas mer utrymme för matte i din beskrivning? Du nämner inte Monte Carlo vilket är Moffens huvudidé?
Jag vet att matematik skrämmer datavetare men som jag sagt tidigare så kan vi rimligtvis utgå från antagandet att eleven som läser förslagen gillar matte?
Qetsiyah skrev:De här förslagen gillar jag! Men jag undrar om inte samma personer ovan också kommer säga att dessa förslag är för svåra?
- Den enda statistiken man lär sig i ma1-ma5 är en pytteliten bit i matte1 och sannolikhetslära i ma5.
- För Brownsk rörelse behövs väl en lagom dos äkta analys i form av måtteori? Och åtminstone lite flervariabelanalys?
I vilken utsträckning går det att hoppa över formella detaljer för att komma till det saftiga man kan leka runt med? Jag är inte insatt i det här ämnet så du får förklara.
Det känns som att i alla fall den där grundläggande statistiken behöver förklaras ordentligt (s.v., väntev, stora talens lag som du skrev, men också varians, multivariabla s.v.? ). Hur mycket numeriska metoder tänker du dig att man behöver?
Ja, om man vill ta med alla detaljer så blir det definitivt ganska mycket att göra. Beroende på om eleven vill inrikta arbete mot matematik eller "programmering"/implementering av en Monte Carlo metod så blir det väldigt olika arbeten (och den mest ambitiösa som vill göra både och).
Om man bara vill implementera och leka runt med prissättningen i sig och hur den beror på olika parametrar säg, så behöver man inte så mycket bakgrund som man kanske tror (eleven har möjligtvis lite svårt att förstå just varför priset kan beräknas på detta sättet, men jag tänker mig att en handviftning med ett par rimliga argument räcker här). Det bör (ungefär) räcka med att veta matematiken bakom
- Stokastisk variabel
- Normalfördelning
- Väntevärde
- Stora talens lag
Och detta är alltså i en dimension, så eleven bör vid det här laget (speciellt om man väljer detta som ett gymnasiearbete) ha koll på funktioner och integraler, så det är nog inte alldeles för mycket (inga bevis behövs eller liknande, idén är ju att få sätta igång med prissättningen så fort som möjligt). Det som blir väldigt nytt är väl Monte Carlo-metoder. Om man lägger lite tid på det så bör det i sin enklaste form inte vara alltför mycket hoppas jag. Till sist behöver man bara förklara köp-/säljoptioner (enkelt koncept), och ge ett handviftande argument om riskneutral värdering. Angående riskneutral värdering så behöver man absolut inte gå djupt. Det räcker med att veta att priset (vanligtvis) ges av riskneutral värdering, och att det innehåller ett väntevärde, så att det är tydligt att vi kan använda Monte Carlo (tack vare stora talens lag).
Jag tänker mig att Brownsk rörelse inte behöver förklaras så mycket matematiskt (om man inte väljer modeller utan en sluten formel, så förslagsvis så håller man sig till geometrisk brownsk rörelse), utan ge en intuition om vad det är och hur den beter sig. Allt som behöver användas i prissättningen är att den är normalfördelad med varians lika med tiden som förflutit.
Angående hur mycket numeriska metoder så är det vanlig Monte Carlo i sin enklaste form (vilket definitivt räcker för ett bra gymnasiearbete beroende på frågeställning).
- Simulera många tal
- Beräkna något med hjälp av dessa simulerade tal
- Medelvärde
Det är allt som behövs i just implementeringen av den numeriska metoden.
Jag vill ju gärna tro att det inte är alltför orimligt för en lite ambitiösare elev, men samtidigt måste jag erkänna att jag kommer inte själv ihåg min egen "matematiska kapacitet" vid den tiden. Det bör vara helt godtagbart att hoppa över många matematiska detaljer och ge rimliga handviftande argument.
Får jag lägga in det i tråden? :)
Hmm, ja, men jag måste säga att det låter väldigt separerat från det jag skrev i den mening att (med reservation för att jag verkligen inte är en expert på detta) förutse pris av aktien är helt annat än prissättningen av ett derivat. För aktien kan jag tänka mig att man använder exempelvis tidsserier eller liknande, och då blir det helt enkelt modellering istället för numeriska metoder som Monte Carlo (som då förutsätter en modell för hur aktien i sig beter sig). Möjligtvis att projektet bör ha som huvudfokus numeriska metoder och Monte Carlo-metoder, men att vad man vill använda det på är valfritt. Jag har bara gett ett ingående förslag hur man kan använda det för att prissätta derivat, men man kan använda det till otroligt mycket annat också.
Det beror alltså helt på vad eleven är intresserad av. Om matematiken är i fokus så kan man fokusera mer på metoden i sig och matematiken bakom, och om man är mer intresserad av finansiella derivat och den faktiska implementeringen så kan man hoppa över många detaljer så länge man har några rimliga argument och lite handviftande.
Detta var bara min idé om hur man kan använda Monte Carlo-metoder, men självklart kanske eleven hellre vill ge sig på exempelvis lite svårare integraler (flerdimensionella?) och för att beräkna några intressanta sådana kan man också använda sig av Monte Carlo-metoder. Här kan eleven med fördel analysera metoden i sig och förklara i vilka fall metoden är lämplig att använda, för och nackdelar.
(Just det, aktier och derivat betyder inte samma, krångligt...)
Okej... Verkar vara ganska lättillgängligt ändå.
Jag kom på en sak, jag undrar om inte det skulle vara nice alternativ även för mattenyfikna ekonomielever i gymnasiet? Då har de dock bara läst upp till matte 3, men har desto bättre koll på den ekonomiska biten?
Jag tänker på den här bilden jag fick från en vän, om hur man blir rik som matematiker, och den vägen är ju svår.
Hmm, ja, men jag måste säga att det låter väldigt separerat från det jag skrev i den mening att (med reservation för att jag verkligen inte är en expert på detta) förutse pris av aktien är helt annat än prissättningen av ett derivat.
Det beror mest på att jag inte är hundra på sådana termer, och dessutom läste lite slarvigt. 😅 Blir det mer korrekt om vi byter aktier mot derivat? :)
(Matematik/programmering) Handeln med finansiella derivat innehåller många matematiska verktyg, exempelvis Monte Carlo-metoden. Hur fungerar sådana metoder, och varför? Du kan exempelvis jämföra olika Monte Carlo-metoder, eller undersöka hur väl Monte Carlo-metoder fungerar när det gäller just finansiella derivat. Liknande förslag finns även här[länk till ditt första inlägg].
Låter det bättre? :)
Jag vet att matematik skrämmer datavetare men som jag sagt tidigare så kan vi rimligtvis utgå från antagandet att eleven som läser förslagen gillar matte?
Tack för den härskartekniken!
Ja, vi kan utgå från att eleverna som läser förslagen gillar matte. Däremot är det tveksamt hur mycket matte vi kan utgå ifrån att de kan, vilket gör det svårt att ta fram förslag. Jag utgår från att den som skriver förslag i denna tråd någonstans har för avsikt att förslagen ska hamna i megatråden, och för att de ska vara greppbara för alla som läser tråden tror jag att det är bra att sammanfatta relaterade förslag i en kortare text, men gärna med länkar för den som vill läsa vidare. Dessvärre är jag inte särskilt bra på finansmarknaden, och det är inte heller min text jag sammanfattar. Det är därför jag frågar författaren om min sammanfattning är rimlig.
Smutstvätt skrev:Hmm, ja, men jag måste säga att det låter väldigt separerat från det jag skrev i den mening att (med reservation för att jag verkligen inte är en expert på detta) förutse pris av aktien är helt annat än prissättningen av ett derivat.
Det beror mest på att jag inte är hundra på sådana termer, och dessutom läste lite slarvigt. 😅 Blir det mer korrekt om vi byter aktier mot derivat? :)
(Matematik/programmering) Handeln med finansiella derivat innehåller många matematiska verktyg, exempelvis Monte Carlo-metoden. Hur fungerar sådana metoder, och varför? Du kan exempelvis jämföra olika Monte Carlo-metoder, eller undersöka hur väl Monte Carlo-metoder fungerar när det gäller just finansiella derivat. Liknande förslag finns även här[länk till ditt första inlägg].
Låter det bättre? :)
Ja, det låter bättre. Om någon kommer på något annat bra förslag där Monte Carlo används så får man jättegärna bidra med dom idéerna. (Några intressanta specifika integraler som man inte kan lösa analytiskt?). Jag tror även att det finns gott om användning inom fysik också, men jag har absolut ingen koll på detta så om någon har någon bra idé så får ni gärna dela med er :)
Jag kom på en sak, jag undrar om inte det skulle vara nice alternativ även för mattenyfikna ekonomielever i gymnasiet? Då har de dock bara läst upp till matte 3, men har desto bättre koll på den ekonomiska biten?
Ja, kanske det? Är man intresserad så kanske det kan fungera, jag vet dock inte hur ett gymnasiearbete på ekonomiprogrammen ser ut.
Det var någon annan användare här på PA som gjorde ett kandidatarbete på att approximera pi med Monte Carlo, kändes lite för basic men jag kanske har fel.
Jag vet att det finns tillämpningar, eller rättare sagt ganska tight koppling, mellan brownian motion och statistisk mekanik, men jag vet för lite om det för att föreslå nåt.
Jag läste just på brownian motion på wiki och det verkar finnas kopplingar till proteinmodellering vilket är intressant för mitt kandidatex!! Jag kanske skriver nåt bioförslag om det.
Moffen skrev:Ja, det låter bättre. Om någon kommer på något annat bra förslag där Monte Carlo används så får man jättegärna bidra med dom idéerna. (Några intressanta specifika integraler som man inte kan lösa analytiskt?). Jag tror även att det finns gott om användning inom fysik också, men jag har absolut ingen koll på detta så om någon har någon bra idé så får ni gärna dela med er :)
Fixat! :)
Qetsiyah skrev:
Jag läste just på brownian motion på wiki och det verkar finnas kopplingar till proteinmodellering vilket är intressant för mitt kandidatex!! Jag kanske skriver nåt bioförslag om det.
Ja Browninan motions används som ett sätt att beskriva hur makromolekyler (t.ex. protein) rör sig i ett media. Och hur mindre partiklar rör sig i förhållande till större (t.ex. joner/bindande ämnen rör sig på ett proteins yta, eller inuti en av proteinet definierad hålighet). Till viss del kan ju en icke bunden partikel betraktas som i konstant rörelse inuti t.ex. ett protein, även om den miljön är betydligt mer begränsande, och samtidigt mer komplex än en vätska i.o.m. att proteinet själv kan påverkas av partikelns rörelser som kan fortplantas till proteinet (vars rörelser i sin tur kan förstärkas/försvagas och återkoppla till partikeln).
Ha som sagt gärna en idé om vad man kan göra praktiskt med ett arbete och en rimlig idé om processen eleven kommer att ha och att de har något de kan börja med direkt så att de inte fastnar i situationen där man inte vet vad man bör/kan/ska göra.
Med finansiella derivat var det exempelvis för mig oklart om de skulle tanka ner en databas av verklig data och analysera den. Eller om det var meningen att man skulle göra en simulation av en modell? Eller om man skulle läsa universitetstexter och försöka skriva en förklaring på gymnasial nivå av begreppen.
Ideal är handledaren väldigt hands-on i början av arbetet och ger uppvärmningsaktiviteter och visar var man kan börja och sedan i slutet kan släppa eleven friare. Det som annars ofta sker är att man börjat i september men något tema men i januari förstår att eleven inte lyckats göra någonting av substans. De kan fler begrepp, vet lite historia, har läst en kul artikel... men har inte gjort något och vet inte vad de ska skriva. ...och så försöker handledaren desperat att ta in dem i skolan på en lördag för att mäta något eftersom de inte lärt sig göra det själva och som man borde gjort i början.
Vissa elever är självgående och säger i september 'jag tänker kolla på X', behöver ingen handledning, och så lämnar de in något som i alla fall är okej sista veckan. Men det är inte de eleverna som behöver hjälp med en lista av idéer.
Att uppmärksamma områden och saker som är intressanta är förstås också bra men det finns miljoner sådana : )
SeriousCephalopod skrev:Ha som sagt gärna en idé om vad man kan göra praktiskt med ett arbete och en rimlig idé om processen eleven kommer att ha och att de har något de kan börja med direkt så att de inte fastnar i situationen där man inte vet vad man bör/kan/ska göra.
Man måste ändå utgå från att det finns stöd och handledning från skola. Jag tänker inte att Pluggakutens förslag ska/måste innehålla färdiga idéer på frågeställning, metod och material. Det är ju trots allt meningen att eleverna själva i samråd med sin handledare ska utforma och komma fram till. Pluggakutens förslag tänker jag ska vara inspiration och idéer till undersökningsområden. Det är såklart bra att vi kollar att ämnena inte är heöt ogörbara för en gymnasieelev men det behöver inte finnas en konkret färdig plan för hur man ska göra det. Om en elev sedan väljer något av ämnena så kan man ju sen exempelvis skapa en tråd på Pluggakuten för att kunna få hjälp, stöd och tips för att exempelvis hitta en passande frågeställning, metod och material.
Tillägg: 6 feb 2022 14:06
Jag kanske tolkade dig något hårt. Du menar kanske att det är bra om det finns en tanke bakom förslaget om ungefär vad man kan göra, utan att det nödvändigtvis måste formuleras exakt eller detaljerat.
Det kan vara så att våra inlägg inte säger emot varandra.
Hmm ja, megatråden var nog mer tänkt som godis för hjärnan att bli inspirerad av och som springboard att söka grejer själv, inte färdiga planer som du och moffen (delvis jag) har skrivit. Så... lite mer "inspiration" än "förslag".
Min tanke med min lista initiellt va att bara spamma idéer, men jag skrev till en introtext för att guida eftersom matte-gyarb är lite ovanligt (och mina lärare va inte hjälpsamma), och som du säger, det behöver bli nåt utav det.
Vissa elever är självgående och säger i september 'jag tänker kolla på X', behöver ingen handledning, och så lämnar de in något som i alla fall är okej sista veckan. Men det är inte de eleverna som behöver hjälp med en lista av idéer.
Förstår inte din åsyftan här, är eleven flitig eller inte? Betyder "okej" "halvdålig"?
Och jodå, den typen av filig elev kan ju också ha nytta av inspiration. (Det ligger väl lite i "inspirations" natur att det inte är nåt man kan ge sig själv)
Qetsiyah: Förstår inte din åsyftan här, är eleven flitig eller inte? Betyder "okej" "halvdålig"?
Även en självgående elev behöver inte leva upp till sina ambitioner eller kan misslyckas med att nå de mål som de hade från början. Okej betyder vad det betyder: acceptabelt i meningen att eleven kan ta examen utan att examinatorn behöver begå tjänstefel. Reflektionen: På min arbetsplats har några elever 3D-printat raketmunstycken i ett försök att studera munstyckeseffekten. När de försökt testköra en kraftmätning fick de ingenting. Eller rättare sagt uppställningen kunde inte påvisa någon effekt som handledaren var övertygad av och eleverna vet inte riktigt varför. Jag tror att deras arbete blev helt okej men det hade såklart varit bättre om de kunnat påvisa något. Anmärkning: Saker kan inte vara halvdåliga. De är antingen dåliga, okej, eller bra. edit: Jag är inte deras handledare. De kan ha löst problemet. Jag vet bara att det jag hörde från deras handledare var intressant.
Kul idéer finns de många av men till projekts natur är att de alltid är svårare än man tror. Exempel: Stjärnan algol är en dubbelstjärna som dimmar varannan dag. Borde inte vara så svårt att fånga på kamera då många gör det som hobbyprojekt. Man kan göra lite analys av period ljusstyrka osv. Jag var jättenära att föreslå detta som projekt i september som en cool idé för ett gymnasiearbete. [...] Sedan dess har jag försökt göra detta själv och efter tiotals timmar så har jag insett hur vansinnigt mycket svårare det var än jag trodde (bara i fråga om hur mycket man var tvungen att lära sig). Nästa år kanske jag kan handleda någon till att göra det men att ge det blankt hade varit oansvarigt.
Jonto: Man måste ändå utgå från att det finns stöd och handledning från skola. [...] Det är såklart bra att vi kollar att ämnena inte är he[l]t ogörbara för en gymnasieelev men det behöver inte finnas en konkret färdig plan för hur man ska göra det
[...]
Jag kanske tolkade dig något hårt. Du menar kanske att det är bra om det finns en tanke bakom förslaget om ungefär vad man kan göra, utan att det nödvändigtvis måste formuleras exakt eller detaljerat.
Jag läste texten om Monte Carlo och förstod inte vad man skulle göra. Var egentligen inte så mycket mer än det. Monte Carlo är coolt jag tror att om jag visar att 7 rader kod kan ge något som ser ut som en aktiekurva så kan det vara en start för diskussion.
Bild
Visa spoiler
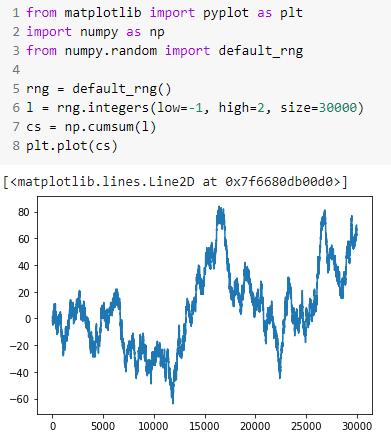
Men bilden ger inte någon fråga att undersöka i sig eller process genom vilken man kan undersöka den.
Mina idéer är inte bättre än era. De är också bara uttryck för mina infall men tänker att de bör kunna sammanfattas i en mening så som "Hur hör X ihop med Y?" och "Detta kommer undersökas genom att...". Förtydliganden: Moffen formulerade några intressanta varför men kan vara att jag vet för lite om finans och att varföret är enklare att förstå/operationalisera än jag tror.
Även en självgående elev behöver inte leva upp till sina ambitioner eller kan misslyckas med att nå de mål som de hade från början. Okej betyder vad det betyder: acceptabelt i meningen att eleven kan ta examen utan att examinatorn behöver begå tjänstefel.
Ja, det var det jag gissade att du menade. "Halvdan" kanske är ett bättre ord. Jag trodde att du också syftade på att eleven gick och skaffade extern handledare.
Du nämner bra exempel på projekt som failade pga dålig planering/tydligt syfte/slutmål men jag ser ingen problematik här utom att vi behöver komma överens vad för syfte våra förslag har (alltså i vilken grad de ska vara "färdiga" för en elev som läser dem). Om de inte är tillräckligt konkreta så får väl eleven i samråd med handledaren göra den mer konkret innan de börjar?
Jag läste texten om Monte Carlo och förstod inte vad man skulle göra. Var egentligen inte så mycket mer än det.
Tråkigt att höra, då verkar det som att jag har misslyckats med att förmedla mina idéer.
Först och främst så lämpar sig ett Monte Carlo arbete till elever som har matematik som ett stort intresse, och att använda eller studera Monte Carlo-metoder är grundidén. Mina förslag är exempel på hur vi kan använda/applicera Monte Carlo specifikt inom finans.
Jag tycker ändå att jag har givit en punktlista på många olika konkreta förslag på vad man kan kolla på. Vad som faktiskt ska göras i gymnasiearbetet måste handledare och eleven klura ut själva.
Själva processen är ganska självklar ur mitt perspektiv, man läser på om vad som behövs för att svara på sin frågeställning (med hjälp av sin handledare), och sen försöker implementera Monte Carlo för att lösa problemet (om man väljer en sån punkt).
Med finansiella derivat var det exempelvis för mig oklart om de skulle tanka ner en databas av verklig data och analysera den. Eller om det var meningen att man skulle göra en simulation av en modell? Eller om man skulle läsa universitetstexter och försöka skriva en förklaring på gymnasial nivå av begreppen.
Det beror helt på vad man bestämmer sig för, vad som låter mest intressant på listan. Men överlag så innebär majoriteten av förslagen att man beräknar priset själv med hjälp av Monte Carlo. Din sista mening är typ vad man kanske kan förvänta sig att eleven ska förstå angående bakgrunden till metoden, men att huvudfokus kan ligga på att jämföra priser beroende på, exempelvis, hur några parametrar ändras. Mina "undersök" är alltså mestadels "beräkna och jämför".
Angående att projekten oftast är svårare än man tror så lämnar jag ingen åsikt, eftersom jag inte ens kommer ihåg min egen matematiska kapacitet när jag skulle skriva mitt gymnasiearbete. Det är mycket möjligt att mina förslag är aningen för avancerade, och om dom inte passar som gymnasiearbete så är det så, jag är ingen lärare och har inte så bra koll på detta.
I just den här punktlistan så behandlar frågeställningen kanske mer jämförandet av priser (med avseende på olika optioner, olika parametrar etc.), och mindre själva matematiken, om det är det du tänker på?
Är det något som jag bör försöka förtydliga ytterligare?
Inser att jag är sent in i diskussionen men här är några tankar och idéer.
1) Jag är av den bestämda åsikten att ett gymnasiearbete i matematik ska bygga på experimentellt arbete. Det räcker inte med att läsa in sig på ett bevis och presentera det. Det fungerade på den tiden det hette specialarbete, men vi har gått vidare från det.
2) Experimentellt arbete kan i matematiken innebära exempelvis programmering, där du kan genomföra experimentella sannolikhetsstudier på olika situationer med Monte Carlometoden. Jag hade en elev som undersökte hur fördelningen av antalet plockade kulor fram till dess någon ropar bingo varierade med storleken på bingorutan.
3) Experimentellt arbete kan också fås genom att undersöka geometriska figurer i t.ex. GeoGebra. Se t.ex. projektidén "Former i Former på https://geogebra.se/gy/ Där finns f.ö en hel massa förslag på vad du kan göra för gymnasiearbete.
4) Om du är modig kan du ställa upp ett system av differentialekvationer som beskriver en situation, lösa systemet med t.ex. GeoGebra och/eller Wolfram Alpha och sedan studera hur lösningarna beter sig då du varierar parametrarna med glidare i GeoGebra. Exempel på dessa finns också på länken ovan.
Frågor om GeoGebra och hur det fungerar etc kan riktas till mig, men studera gärna innehållet på https://geogebra.se och den länkade youtubekanalen först.
Jonas Hall skrev:Inser att jag är sent in i diskussionen men här är några tankar och idéer.
1) Jag är av den bestämda åsikten att ett gymnasiearbete i matematik ska bygga på experimentellt arbete. Det räcker inte med att läsa in sig på ett bevis och presentera det. Det fungerade på den tiden det hette specialarbete, men vi har gått vidare från det.
2) Experimentellt arbete kan i matematiken innebära exempelvis programmering, där du kan genomföra experimentella sannolikhetsstudier på olika situationer med Monte Carlometoden. Jag hade en elev som undersökte hur fördelningen av antalet plockade kulor fram till dess någon ropar bingo varierade med storleken på bingorutan.
3) Experimentellt arbete kan också fås genom att undersöka geometriska figurer i t.ex. GeoGebra. Se t.ex. projektidén "Former i Former på https://geogebra.se/gy/ Där finns f.ö en hel massa förslag på vad du kan göra för gymnasiearbete.
4) Om du är modig kan du ställa upp ett system av differentialekvationer som beskriver en situation, lösa systemet med t.ex. GeoGebra och/eller Wolfram Alpha och sedan studera hur lösningarna beter sig då du varierar parametrarna med glidare i GeoGebra. Exempel på dessa finns också på länken ovan.
Frågor om GeoGebra och hur det fungerar etc kan riktas till mig, men studera gärna innehållet på https://geogebra.se och den länkade youtubekanalen först.
Du är inte alls sen in, utan tanken är just att man kan bygga på med idéer och tankar. Många elever har sitt gymnasiearbete framför sig.
Tack för bra idéer och reflektioner.
Bra hemsida, många coola förslag!
Däremot what is this abomination
Kan det vara en märkligt beskuren version av
där opp/hip är en förkortning av opposite / hypotenuse? Oavsett... mina ögon blöder. Börjar likna den där sfären i Las Vegas med sin egen version av pi. 😂









