Sfäriska koordinaterna
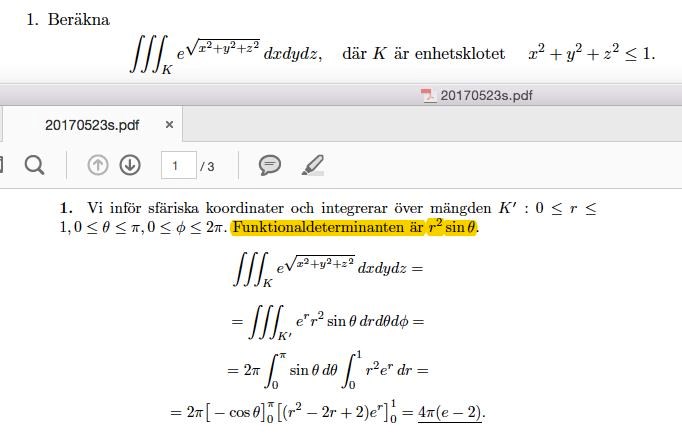
Jag hänger inte med på gränser det är ju en halvsfär då går alltid z bara från ? Helsfär ?
Det står ju tydligt att det är enhetsklotet.
Eller menar du att även bör gå mellan ? Det måste den inte. Tänk om du enbart hade och . Då har du en halv cirkelskiva. Låter du nu den halvcirkeln rotera 360 graders så får du har du ett enhetsklot. Alltså krävs , och .
Om du istället ritade en hel cirkelskiva, säg och så har du en hel cirkelskiva. Då behöver du enbart rotera den 180 grader för att få ett klot igen, alltså fortfarande . Annars "överlappar" du det som redan finns.
woozah skrev:Eller menar du att även bör gå mellan ? Det måste den inte. Tänk om du enbart hade och . Då har du en halv cirkelskiva. Låter du nu den halvcirkeln rotera 360 graders så får du har du ett enhetsklot. Alltså krävs , och .
Om du istället ritade en hel cirkelskiva, säg och så har du en hel cirkelskiva. Då behöver du enbart rotera den 180 grader för att få ett klot igen, alltså fortfarande . Annars "överlappar" du det som redan finns.
Okej, så om, om vi hade en kvartscirkelskiva då skulle $$\theta in [0, 2\pi]$$
Det här med sfäriska koordinater är det lite klurigt. För att beskriva enhetssfären har vi gränserna , och (notera att facit byter plats på bokstäverna och , jag använder Wikipedias beteckningar).
Vi kan tänka oss detta som att vi börjar med att rita upp en halv cirkelskiva (motsvarande gränserna och ) och därefter roterar den ett helt varv () kring -axeln:

vilket ger oss en hel sfär:

Om vi nu ville ha en halvsfär med skulle vi justera gränserna för till att vara :

och roterar vi detta ett helt varv () kring z-axeln får vi vår halvsfär:

AlvinB skrev:Det här med sfäriska koordinater är det lite klurigt. För att beskriva enhetssfären har vi gränserna , och (notera att facit byter plats på bokstäverna och , jag använder Wikipedias beteckningar).
Vi kan tänka oss detta som att vi börjar med att rita upp en halv cirkelskiva (motsvarande gränserna och ) och därefter roterar den ett helt varv () kring -axeln:
vilket ger oss en hel sfär:
Om vi nu ville ha en halvsfär med skulle vi justera gränserna för till att vara :
och roterar vi detta ett helt varv () kring z-axeln får vi vår halvsfär:
hmmmm okej, tror jag hänger med.
Men jag tänker om det finns ett förållande mellan theta och fi (enl. wikipedias betckningar) som mer eller mindre alltid fungerar?
Jag begriper inte riktigt vad du menar med förhållande mellan theta och fi.
Hela poängen är ju att variablerna är oberoende av varandra så att man kan beskriva volymer (som kräver tre oberoende variabler).
AlvinB skrev:Jag begriper inte riktigt vad du menar med förhållande mellan theta och fi.
Hela poängen är ju att variablerna är oberoende av varandra så att man kan beskriva volymer (som kräver tre oberoende variabler).
Jahaa jag trodde dom hängde ihop :)
men om vi tar lite exempel då:
Ex 1.
Detta är ju då ett halvt klot? och därför går theta (ej wikipedias beteckningar nu) [0,pi]
Var står det att det är ett halvt klot?
"klotet " tycker jag ganska tydligt säger att det är hela klotet som avses.
mrlill_ludde skrev:AlvinB skrev:Jag begriper inte riktigt vad du menar med förhållande mellan theta och fi.
Hela poängen är ju att variablerna är oberoende av varandra så att man kan beskriva volymer (som kräver tre oberoende variabler).
Jahaa jag trodde dom hängde ihop :)
men om vi tar lite exempel då:
Ex 1.
Detta är ju då ett halvt klot? och därför går theta (ej wikipedias beteckningar nu) [0,pi]
Varför får du för dig att det är ett halvt klot? Det är såvitt jag kan se ett "helt" klot.
AlvinB skrev:Var står det att det är ett halvt klot?
"klotet " tycker jag ganska tydligt säger att det är hela klotet som avses.
Ahhh nej jag läste bara och därför tänkte jag att det var halvklot.
Moffen skrev:mrlill_ludde skrev:AlvinB skrev:Jag begriper inte riktigt vad du menar med förhållande mellan theta och fi.
Hela poängen är ju att variablerna är oberoende av varandra så att man kan beskriva volymer (som kräver tre oberoende variabler).
Jahaa jag trodde dom hängde ihop :)
men om vi tar lite exempel då:
Ex 1.
Detta är ju då ett halvt klot? och därför går theta (ej wikipedias beteckningar nu) [0,pi]Varför får du för dig att det är ett halvt klot? Det är såvitt jag kan se ett "helt" klot.
Ahhh nej jag läste bara och därför tänkte jag att det var halvklot.
Om du vill ha ett algebraiskt sätt att ta fram gränserna kan du resonera så här:
I Wikipedia-betecknade sfäriska koordinater gäller alltid följande olikheter (dessa olikheter beskriver hela ):
Om vi nu vill beskriva ett helt klot har vi då det kartesiska sambandet . Ur det får vi:
Tillsammans med de övre olikheterna får vi:
som alltså beskriver ett helt klot. Lägger vi till villkoret (d.v.s. vi gör om det till ett halvklot) får vi:
vilket tillsammans med ger att eftersom då , alltså beskrivs ett halvklot med positiv -komponent med:
AlvinB skrev:Om du vill ha ett algebraiskt sätt att ta fram gränserna kan du resonera så här:
I Wikipedia-betecknade sfäriska koordinater gäller alltid följande olikheter (dessa olikheter beskriver hela ):
Om vi nu vill beskriva ett helt klot har vi då det kartesiska sambandet . Ur det får vi:
Tillsammans med de övre olikheterna får vi:
som alltså beskriver ett helt klot. Lägger vi till villkoret (d.v.s. vi gör om det till ett halvklot) får vi:
vilket tillsammans med ger att eftersom då , alltså beskrivs ett halvklot med positiv -komponent med:
Gäller samma beräkningar/tänk med ellipser och elippsoioder?
Vill bara säga att AlvinB visade geometriskt exakt det jag ville förklara. Fint! :)
mrlill_ludde skrev:
Gäller samma beräkningar/tänk med ellipser och elippsoioder?
Det fungerar alldeles utmärkt. Om du har en enhetssfär så får du att är, i sfäriska koordinater, . (använd lite trig-ettor etc så får du detta resultat).
Om du istället befinner dig på ellipsoiden så kan du manipulera -uttrycket i de sfäriska koordinaterna för att återigen få en vanligt enhetssfär. Tänk t.ex. i stil med:
.
Nu får du (om du sätter in från ovan) bara att . M.h.a. koefficienten 1/2 i z-transformationen så har du "dragit ihop" ellipsoiden så att den istället blir en sfär.
Tänk på att när du ändrar de sfäriska koordinaterna får du andra Jacobianer, som nu inte bara är .
woozah skrev:mrlill_ludde skrev:
Gäller samma beräkningar/tänk med ellipser och elippsoioder?
Det fungerar alldeles utmärkt. Om du har en enhetssfär så får du att är, i sfäriska koordinater, . (använd lite trig-ettor etc så får du detta resultat).
Om du istället befinner dig på ellipsoiden så kan du manipulera -uttrycket i de sfäriska koordinaterna för att återigen få en vanligt enhetssfär. Tänk t.ex. i stil med:
.
Nu får du (om du sätter in från ovan) bara att . M.h.a. koefficienten 1/2 i z-transformationen så har du "dragit ihop" ellipsoiden så att den istället blir en sfär.
Tänk på att när du ändrar de sfäriska koordinaterna får du andra Jacobianer, som nu inte bara är .

denna va?
Nja, det där är för elliptiska koordinater i två dimensioner.
Nu diskuterar vi ellipsoidiska koordinater i tre dimensioner.
Ett trick du kan använda är att om du vet att determinanten (Wikipedia-beteckningar) så kommer den nya determinanten att bli samma sak delat på två, eftersom du multiplicerat en rad av derivator med .
AlvinB skrev:Nja, det där är för elliptiska koordinater i två dimensioner.
Nu diskuterar vi ellipsoidiska koordinater i tre dimensioner.
Ett trick du kan använda är att om du vet att determinanten (Wikipedia-beteckningar) så kommer den nya determinanten att bli samma sak delat på två, eftersom du multiplicerat en rad av derivator med .
Men men... exempel 3 här på sid 3. men kom på det, du sa delat med 2 i en annan tråd. Men ex då? Fel?
I det där exemplet integrerar man först i -led (som med din metod här) så att man blir kvar med bara en dubbelintegral. Först då gör man ett variabelbyte och går över till elliptiska koordinater. Det är alltså ett variabelbyte för en dubbelintegral man gör där. Man använder inte sfäriska koordinater över huvud taget.
I vissa fall där man har enkla integrander (i exemplet söker man volymen och har därmed integranden ) kan man ju göra så att man integrerar separat och först då gör ett variabelbyte, men då är det inte sfäriska koordinater som är aktuella eftersom man får kvar en tvådimensionell integral.
AlvinB skrev:I det där exemplet integrerar man först i -led (som med din metod här) så att man blir kvar med bara en dubbelintegral. Först då gör man ett variabelbyte och går över till elliptiska koordinater. Det är alltså ett variabelbyte för en dubbelintegral man gör där. Man använder inte sfäriska koordinater över huvud taget.
I vissa fall där man har enkla integrander (i exemplet söker man volymen och har därmed integranden ) kan man ju göra så att man integrerar separat och först då gör ett variabelbyte, men då är det inte sfäriska koordinater som är aktuella eftersom man får kvar en tvådimensionell integral.
Ahhh!! :) Oki! trorr allt börjar klarna nu
AlvinB skrev:I det där exemplet integrerar man först i -led (som med din metod här) så att man blir kvar med bara en dubbelintegral. Först då gör man ett variabelbyte och går över till elliptiska koordinater. Det är alltså ett variabelbyte för en dubbelintegral man gör där. Man använder inte sfäriska koordinater över huvud taget.
I vissa fall där man har enkla integrander (i exemplet söker man volymen och har därmed integranden ) kan man ju göra så att man integrerar separat och först då gör ett variabelbyte, men då är det inte sfäriska koordinater som är aktuella eftersom man får kvar en tvådimensionell integral.
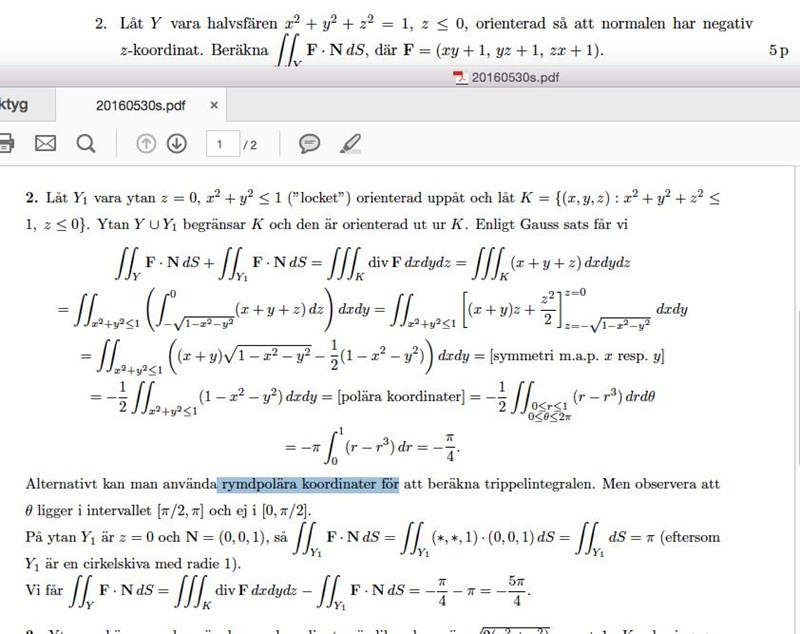
Men hur blir det med denna då, i sfäriska?? Illustrerat? För denna är ju en halvsfär när allt ligger ovanför 1?
Nej, halvsfären har z-koordinater som är lika med eller mindre än 0. Ingenting är större än 1 på något håll. Hade du tänkt lägga in en annan uppgift?
Smaragdalena skrev:Nej, halvsfären har z-koordinater som är lika med eller mindre än 0. Ingenting är större än 1 på något håll. Hade du tänkt lägga in en annan uppgift?
Jag tänkte på fel uppg? Men jag menar ändå denna.
För om z är mindre 0. Försöker tänka mig detta i 3D, och försöker förstå varför den går fr pi till pi/2?
Alltså ”backar”??
För att det skall gå åt samma håll som när växer från 0 till 1.



