Hitta skuggade områdets area
Hej allihopa!
Jag undrade bara om hur ni skulle gå tillväga till att lösa den här uppgiften: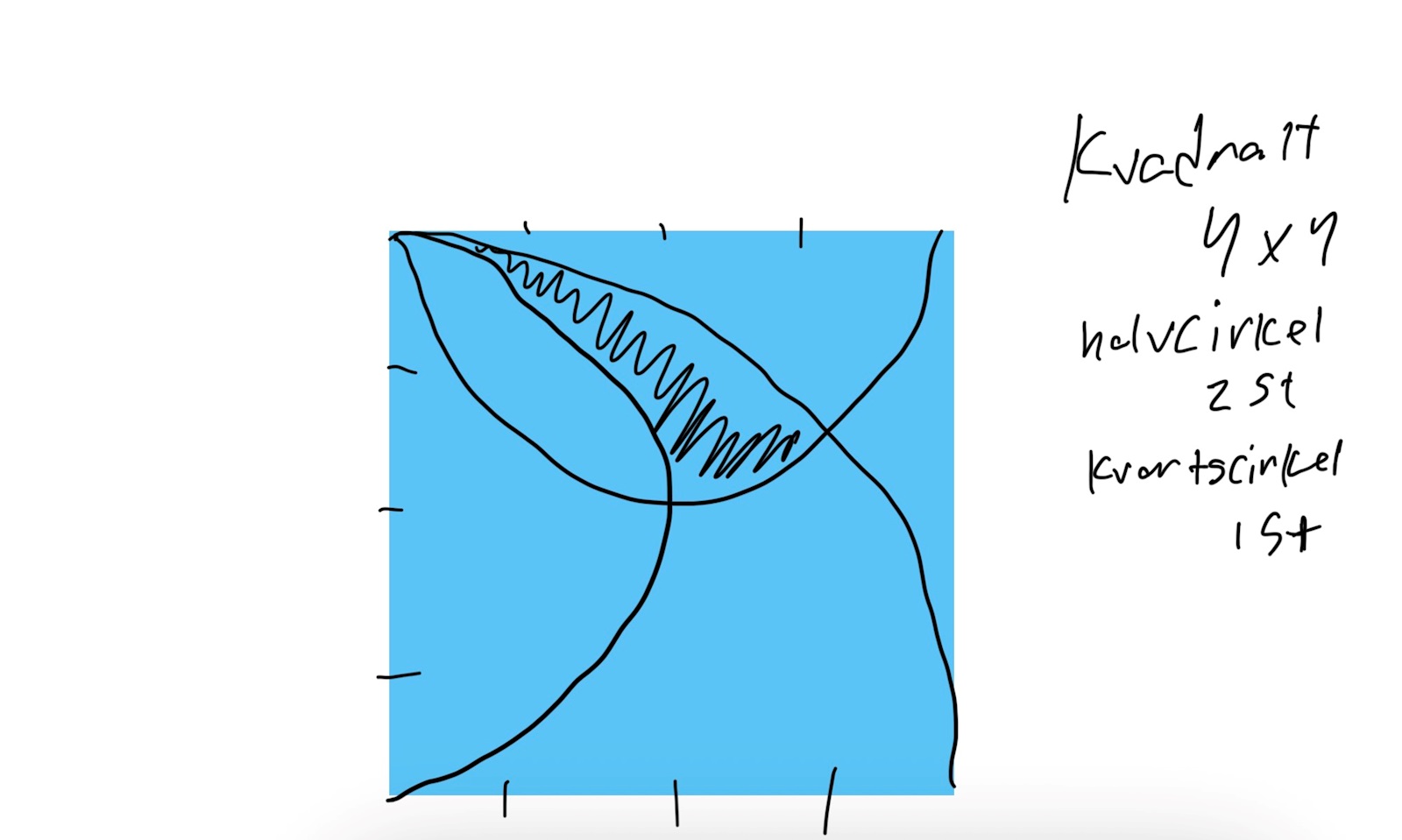 Fick det här från en av mina vänner då jag ville ha en liten brainteaser. Dock har jag suttit med den här uppgiften nästan hela dagen och inte fattat hur man skulle kunna få fram arean!
Fick det här från en av mina vänner då jag ville ha en liten brainteaser. Dock har jag suttit med den här uppgiften nästan hela dagen och inte fattat hur man skulle kunna få fram arean!
Jag skulle vilja bara veta hur jag skulle kunna börja med uppgiften, men inte att ni löser det åt mig utan ger mig "ledtråd" så att jag kan vidareutveckla lösningen framåt.
Har jag förstått uppgiften rätt?
Vi har en kvadrat på 4x4 längdenheter. Från övre vänstra hörnet till övre högra hörnet går en halvcirkel. Likaså går en halvcirkel från övre vänstra till nedre vänstra hörnet. Slutligen går en kvartscirkel från övre vänstra till nedre högra hörnet. Bestäm arean av det område som avgränsas av dessa halv/kvarts-cirklar.
thedifference skrev:Har jag förstått uppgiften rätt?
Vi har en kvadrat på 4x4 längdenheter. Från övre vänstra hörnet till övre högra hörnet går en halvcirkel. Likaså går en halvcirkel från övre vänstra till nedre vänstra hörnet. Slutligen går en kvartscirkel från övre vänstra till nedre högra hörnet. Bestäm arean av det område som avgränsas av dessa halv/kvarts-cirklar.
Ja, exakt! Det skuggade området (det område som avgränsas) är det vi vill hitta.
All information du har sagt stämmer.
Hej! Jag har läst igenom tråden och tänkte lite på om man kunde göra det med integraler. Dock vet jag inte riktigt hur jag får fram funktionerna som beskriver kurvorna i kvadraten. Jag har tänkt lite så här: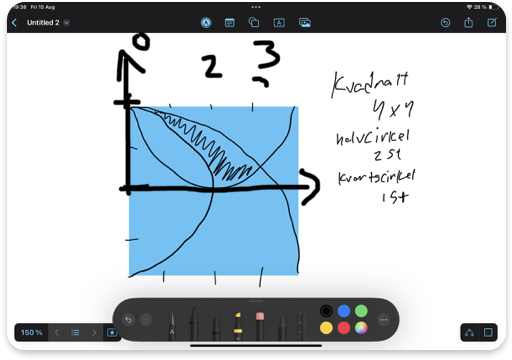 Med det här så tänker jag att en av kurvorna kan beskrivas som y = sqrt(4-x^2), men de andra två kurvor vet jag inte riktigt hur jag får fram. Integralberäkningen därefter borde vara lätt för mig. Det jag fick fram är ekvationen på en av halvcirklarna (som går från övre vänstra till nedre vänstra hörnet).
Med det här så tänker jag att en av kurvorna kan beskrivas som y = sqrt(4-x^2), men de andra två kurvor vet jag inte riktigt hur jag får fram. Integralberäkningen därefter borde vara lätt för mig. Det jag fick fram är ekvationen på en av halvcirklarna (som går från övre vänstra till nedre vänstra hörnet).
Den övre halvcirkeln definieras väl av ekvationen genom att kolla i figuren och kvartscirkeln borde väl definieras av ?
naytte skrev:Den övre halvcirkeln definieras väl av ekvationen genom att kolla i figuren och kvartscirkeln borde väl definieras av ?
Var lite längesedan jag använde cirkelns formel… men jag förstår inte varför halvcirkeln har en annan ekvation och kvartscirkeln någon annan? Skulle du kunna förklara kanske?
Sökte upp precis... aj, okej jag får tänka lite men jag tror nog jag löser det vi får se
Det ser lite udda ut när jag lägger det i Desmos... Använder det bara för att se om jag får rätt funktioner och så.
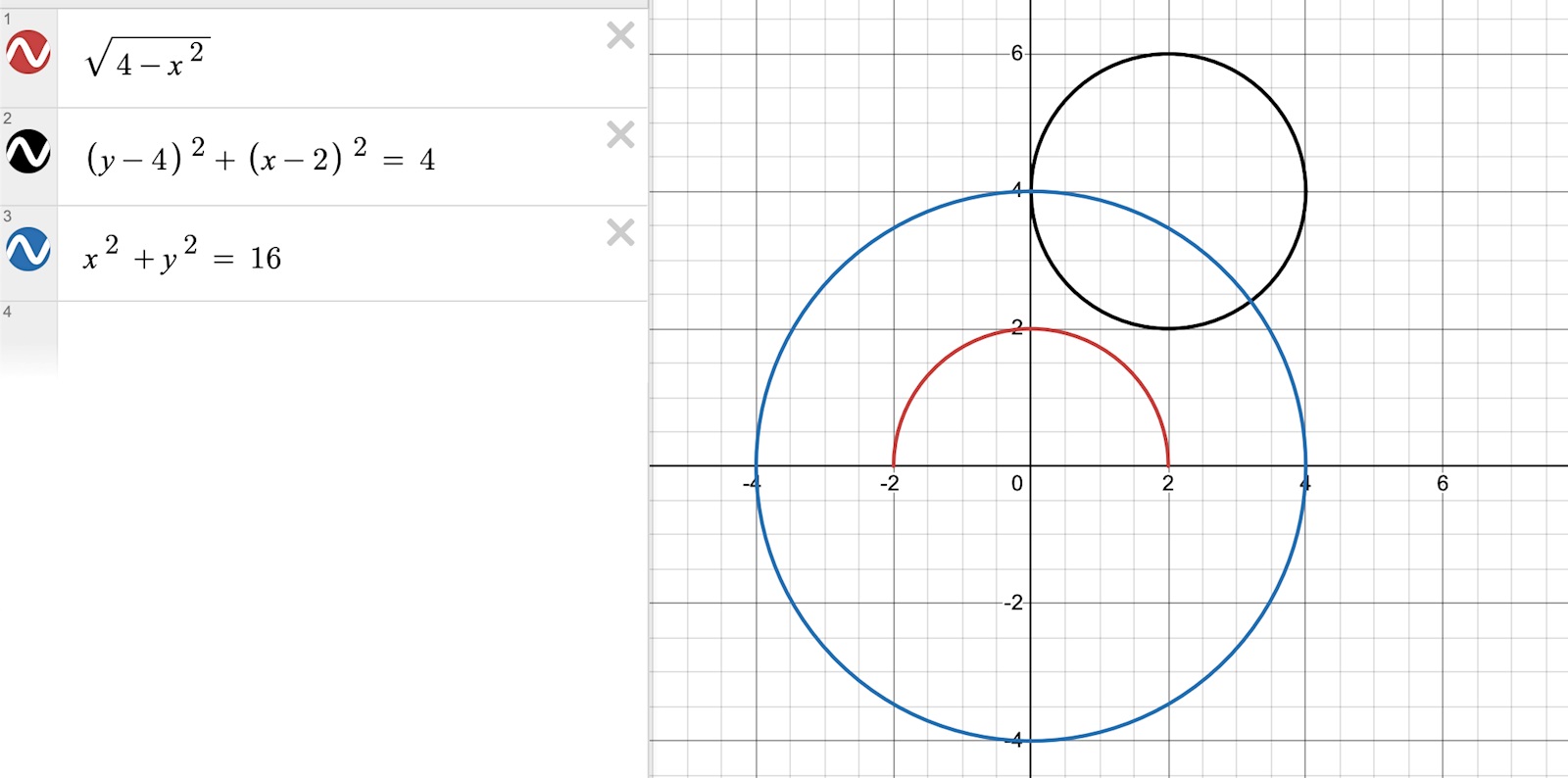
EDIT: När jag lekte lite så såg jag det här: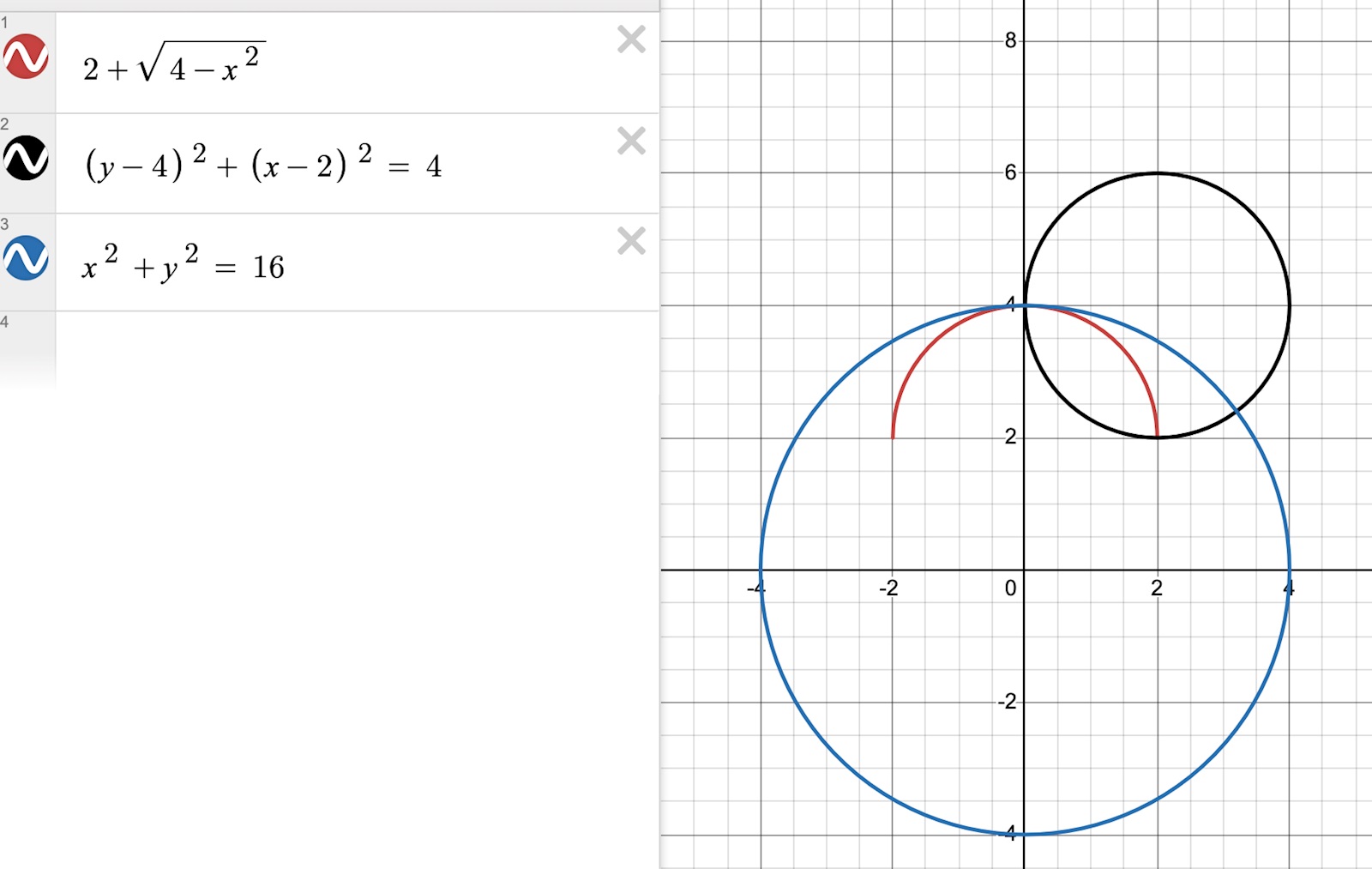 Det ser ju ut som att det passar in, men jag undrade typ om det finns ett sätt för mig att göra det redan vid första försöket utan att typ "passa in" eller använda brute force för att få fram det?
Det ser ju ut som att det passar in, men jag undrade typ om det finns ett sätt för mig att göra det redan vid första försöket utan att typ "passa in" eller använda brute force för att få fram det?
Detta kanske inte hjälper mycket men sättet jag löste problemet på var att dela upp figuren på mitten och sedan göra integralberäkningar för att hitta värdet på zonen.
Ekvationen du kom fram till för den röda kurvan stämde inte, det är därför du var tvungen att lägga till en konstant för att få det att se rätt ut
naytte skrev:Ekvationen du kom fram till för den röda kurvan stämde inte, det är därför du var tvungen att lägga till en konstant för att få det att se rätt ut
Kom på det precis så gjorde det här istället:
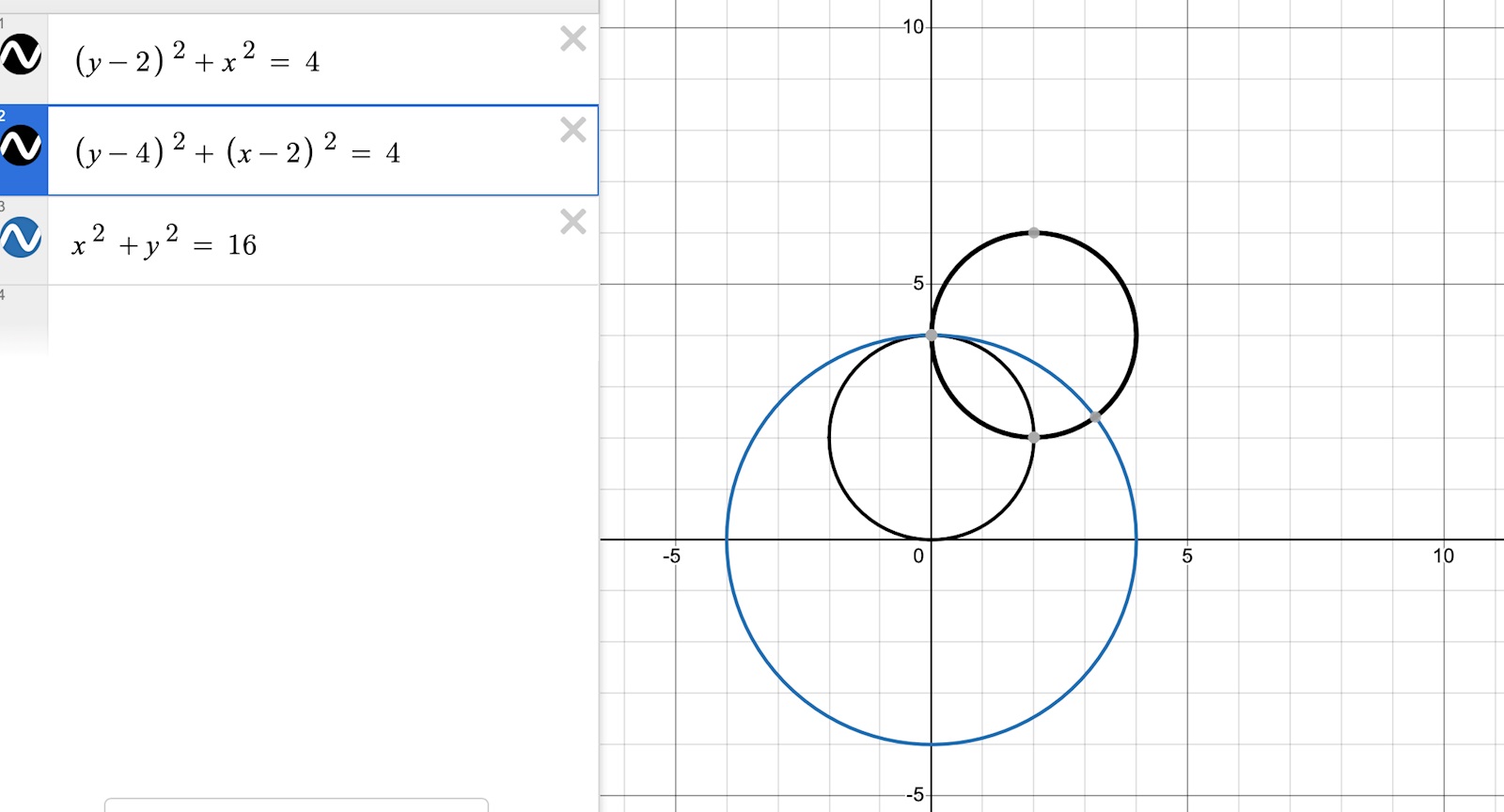
Så där ja, nu ser det rätt ut!
Nu är det bara att integrera. Med kunskaper ur Ma4 kan du göra detta med en summa av två integraler.
Jag tänker det här: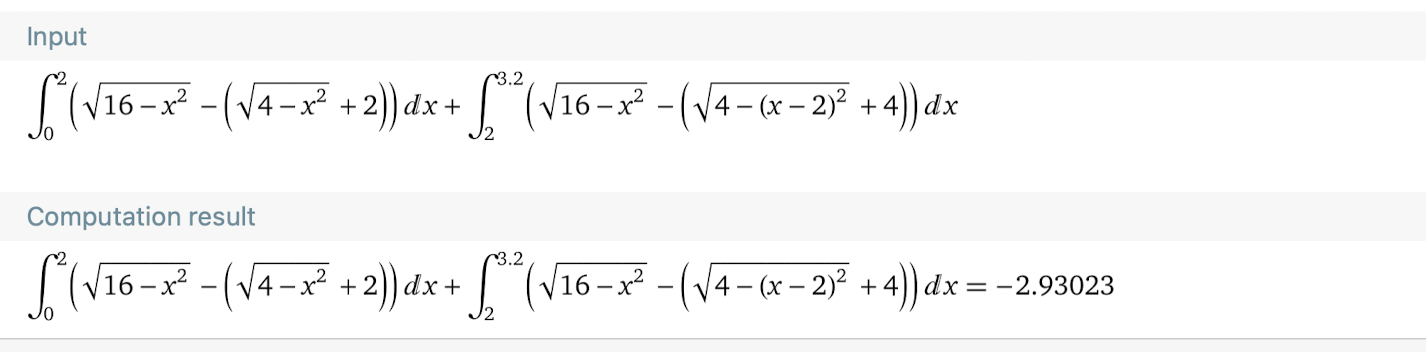 Jag förstår dock inte vad som är fel här? Kan ju inte ha en negativ area...
Jag förstår dock inte vad som är fel här? Kan ju inte ha en negativ area...
Det jag gör är att hitta skillnaden mellan två funktioner och sedan bara integrera.
Du tar fel del av kurvan som definieras av när du integrerar. Det är den nedre delen av kurvan som är relevant så integranden i den andra integralen måste vara
naytte skrev:Du tar fel del av kurvan som definieras av när du integrerar. Det är den nedre delen av kurvan som är relevant så integranden i den andra integralen måste vara
Hur fick du fram det som integranden?
Om du löser ut i ekvationen får du två lösningar, eller hur? En lösning definierar cirkelns övre halva, och en definierar cirkelns undre halva. Det är den undre halvan som är aktuell för oss.
naytte skrev:Om du löser ut i ekvationen får du två lösningar, eller hur? En lösning definierar cirkelns övre halva, och en definierar cirkelns undre halva. Det är den undre halvan som är aktuell för oss.
Ahh just det! Jag tog ju den positiva roten när jag tog kvadratroten ur (y-4)^2, men vi vill ju ha den negativa roten!
Exakt!

Om jag har tänkt rätt så borde det vara svaret, ungefär 1.56 a.e
Ingen aning om det är rätt men svaret är ju positivt i alla fall så det är ett gott tecken :)
75 arctan(1/2) - 25 är det exakta svaret i versionen av uppgiften där kvadratens sida är 10 le.
Omräknat blir det precis det värde du fick.



